高校数学Ⅱ『図形と方程式』で学ぶ『2円の交点を通る直線・円』について解説!
苦手な人が多い問題としても有名です!
この投稿を見れば、『2円の交点を通る直線・円』に関する問題はバッチリ!
2円の交点を通る直線または円
2円 $x^2+y^2+lx+my+n$$=0$,$x^2+y^2+l’x+m’y+n’$$=0$ が異なる2点で交わるとき,
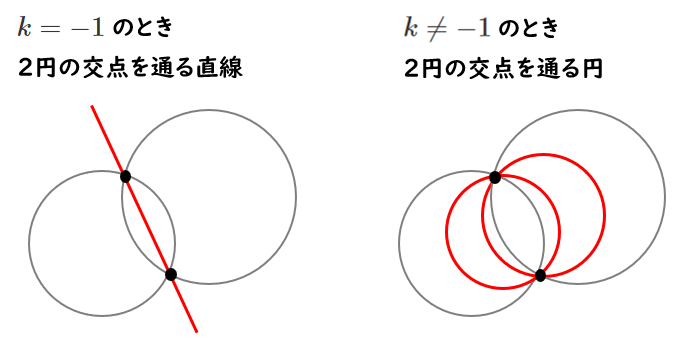
$($$x^2+y^2+lx+my+n$$)+k($$x^2+y^2+l’x+m’y+n’$$)=0$ ($k$ は実数)
は, $k=-1$ のとき,2つの交点を通る直線を表す
$k≠-1$ のとき,2つの交点を通る円を表す
(ただし、$x^2+y^2+l’x+m’y+n’=0$ を除く)
例えば、
2円 $x^2+y^2-10$$=0$ と $x^2+y^2+2x-2y-6$$=0$ の交点を通る直線または円は
$($$x^2+y^2+2x-2y-6$$)+k($$x^2+y^2-10$$)=0$ ($k$ は実数) と表せる
ただし、$x^2+y^2-10=0$ を除く
【補足】簡単な方に $k$ をつける方がよい(ここでは $x^2+y^2-10$)
2円 $x^2+y^2-10=0$ と $x^2+y^2+2x-2y-6=0$ の交点は
\begin{eqnarray} \left\{ \begin{array}{l} x^2+y^2-10=0 \\ x^2+y^2+2x-2y-6=0 \end{array} \right. \end{eqnarray}の解である
これを解くと,$(-3,-1)$,$(1,3)$
$(x^2+y^2+2x-2y-6)+k(x^2+y^2-10)=0$ に $(-3,-1)$ を代入すると
$\{(-3)^2+(-1)^2+2\cdot(-3)-2\cdot(-1)-6\}+k\{(-3)^2+(-1)^2-10\}=0$
等式が成り立つ
$(x^2+y^2+2x-2y-6)+k(x^2+y^2-10)=0$ に $(1,3)$ を代入すると
$(1^2+3^2+2\cdot1-2\cdot3-6)+k(1^2+3^2-10)=0$
等式が成り立つ
よって,$(x^2+y^2+2x-2y-6)+k(x^2+y^2-10)=0$ は,2円 $x^2+y^2-10=0$ と $x^2+y^2+2x-2y-6=0$ の交点 $(-3,-1)$,$(1,3)$ を通る
$k=-1$ を代入すると
$(x^2+y^2+2x-2y-6)-(x^2+y^2-10)=0$
すなわち $x-y+2=0$
$k=-1$ のとき,$x^2$ と $y^2$ が消去されて直線の方程式になる
式変形すると $(k+1)x^2+(k+1)y^2+2x-2y+(-10k-6)=0$
$k≠-1$ のとき,$x^2$ と $y^2$ が消去されず円の方程式になる
問題
(1) 2つの交点を通る直線の方程式を求めよ。
(2) 2つの交点と原点を通る円の方程式を求めよ。
2円 $x^2+y^2-4$$=0$ と $x^2+y^2+4x-2y+4$$=0$ の交点を通る直線または円は
$($$x^2+y^2+4x-2y+4$$)+k($$x^2+y^2-4$$)=0$ ($k$ は実数) … ①
ただし,$x^2+y^2-4=0$ は除く
(1) $k=-1$ のとき,①は直線を表すから
$(x^2+y^2+4x-2y+4)-(x^2+y^2-4)=0$
よって $2x-y+4=0$
(2) ①が原点を通るので $4-4k=0$
すなわち $k=1$
$k=1$ を①に代入すると
$(x^2+y^2+4x-2y+4)+(x^2+y^2-4)=0$
整理すると $x^2+y^2+2x-y=0$




コメント