高校数学Ⅱの『図形と方程式』で学ぶ『2円の共通接線』について解説!
円の接線の問題のポイントは、「円の中心と直線の距離=円の半径」という式を作ること!
共通接線のおき方によって、2種類の解法を考えることができる!
この投稿を見れば、『2円の共通接線』はバッチリ!
問題
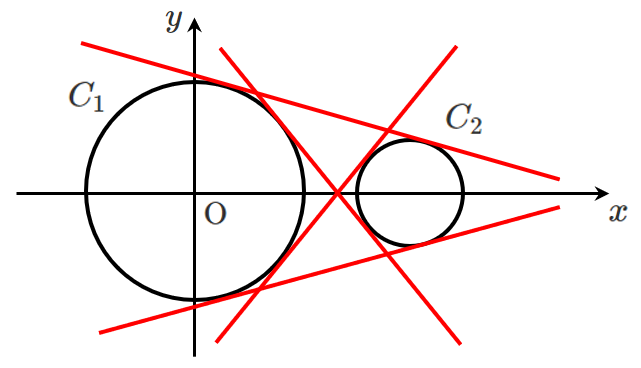
2円が共有点をもたない場合は,共通接線が4本存在する
2円の位置関係における共通接線の本数はこれ↓

ポイント
円の接線に関する問題は、「円の中心と直線の距離=円の半径」という式を作る

解法1:接点の座標をおく
円 $x^2+y^2=r^2$ 上の点 $(p,q)$ における接線の方程式は
$px+qy=r^2$
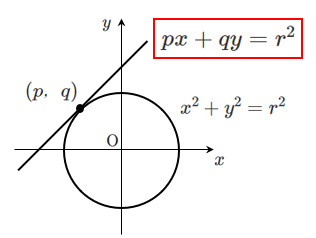
原点を中心とする $C_1$ の接点の座標を $(p,q)$ とおくことで,接線の方程式を表す … ①
➡ 「円の中心と直線の距離=半径」という式を作る … ②
➡ 接点 $(p,q)$ は円 $C_1$ 上にあるという条件から式を作る … ③
②と③を連立して,$p$ と $q$ を求める
①に代入して共通接線を求める
円 $C_1$ 上の接点の座標を $(p,q)$ とおくと
この接点における接線は $px+qy=4$ … ①
円 $C_2$ の中心 $(4,0)$ と $px+qy-4=0$ との距離が円 $C_2$ の半径 $1$ と等しいので
$\displaystyle{\frac{|4p-4|}{\sqrt{p^2+q^2}}=1}$ … ②
また,点 $(p,q)$ は円 $C_1$ 上の点なので
$p^2+q^2=4$ … ③
③を②に代入して $\displaystyle{\frac{|4p-4|}{2}=1}$
$\displaystyle{|p-1|=\frac{1}{2}}$
$\displaystyle{p-1=\pm\frac{1}{2}}$
したがって $\displaystyle{m=\frac{3}{2},\frac{1}{2}}$
③に代入して $\displaystyle{m=\frac{3}{2}}$ のとき, $\displaystyle{n=\pm\frac{\sqrt{7}}{2}}$
$\displaystyle{m=\frac{1}{2}}$ のとき, $\displaystyle{n=\pm\frac{\sqrt{15}}{2}}$
①より,4本の接線の方程式は
$\displaystyle{\frac{3}{2}x\pm\frac{\sqrt{7}}{2}y=4}$,$\displaystyle{\frac{1}{2}x\pm\frac{\sqrt{15}}{2}y=4}$
すなわち $3x\pm\sqrt{7}y=8$,$x\pm\sqrt{15}y=8$
解法2:共通接線の傾きとy切片をおく
共通接線を $y=ax+b$ とおく(傾きを $a$、$y$ 切片を $b$)
※直線の傾きをおく場合は、$y$ 軸と平行な直線を表すことができないので注意が必要
➡ この問題は、求める直線が $y$ 軸と平行な直線にならないことを記述する
円 $C_1$ と $C_2$ のそれぞれについて、「円の中心と直線の距離=円の半径」という式を作って連立することで $a$ と $b$ を求める
$C_1$,$C_2$ の両方に接する直線は $y$ 軸に平行でないので $y=ax+b$
すなわち $ax-y+b=0$ … ①
①が円 $C_1$ に接するので,円 $C_1$ の中心 $(0,0)$ と直線①の距離が円 $C_1$ の半径 $2$ と等しい
$\displaystyle{\frac{|a\cdot0-0+b|}{\sqrt{a^2+(-1)^2}}=2}$
よって $|b|=2\sqrt{a^2+1}$ … ②
②が円 $C_2$ に接するので,円 $C_2$ の中心 $(4,0)$ と直線①の距離が円 $C_2$ の半径 $1$ と等しい
$\displaystyle{\frac{|a\cdot4-0+b|}{\sqrt{a^2+(-1)^2}}=1}$
よって $|4a+b|=\sqrt{a^2+1}$ … ③
②,③より $|b|=2|4a+b|$
ゆえに $b=\pm2(4a+b)$
すなわち $b=-8a$ または $\displaystyle{b=-\frac{8}{3}a}$
[1] $b=-8a$ のとき
②に代入すると $|-8a|=2\sqrt{a^2+1}$
両辺を2乗すると $64a^2=4(a^2+1)$
$\displaystyle{a^2=\frac{1}{15}}$ より $\displaystyle{a=\pm\frac{1}{\sqrt{15}}}$
$b=-8a$ より $\displaystyle{a=\frac{1}{\sqrt{15}}}$ のとき $\displaystyle{b=-\frac{8}{\sqrt{15}}}$
$\displaystyle{a=-\frac{1}{\sqrt{15}}}$ のとき $\displaystyle{b=\frac{8}{\sqrt{15}}}$
[2] $\displaystyle{b=-\frac{8}{3}a}$ のとき
②に代入すると $\displaystyle{|-\frac{8}{3}a|=2\sqrt{a^2+1}}$
両辺を2乗すると $\displaystyle{\frac{64}{9}a^2=4(a^2+1)}$
$\displaystyle{a^2=\frac{9}{7}}$ より $\displaystyle{a=\pm\frac{3}{\sqrt{7}}}$
$\displaystyle{b=-\frac{8}{3}a}$ より $\displaystyle{a=\frac{3}{\sqrt{7}}}$ のとき $\displaystyle{b=-\frac{8}{\sqrt{7}}}$
$\displaystyle{a=-\frac{3}{\sqrt{7}}}$ のとき $\displaystyle{b=\frac{8}{\sqrt{7}}}$
[1],[2] より,①に代入して
$\displaystyle{y=\frac{1}{\sqrt{15}}x-\frac{8}{\sqrt{15}}}$,$\displaystyle{y=-\frac{1}{\sqrt{15}}x+\frac{8}{\sqrt{15}}}$
$\displaystyle{y=\frac{3}{\sqrt{7}}x-\frac{8}{\sqrt{7}}}$,$\displaystyle{y=-\frac{3}{\sqrt{7}}x+\frac{8}{\sqrt{7}}}$
すなわち $x\pm\sqrt{15}y=8$,$3x\pm\sqrt{7}y=8$




コメント