２次不等式｜因数分解

２次不等式の解き方ちゃんとわかっていますか？

２次不等式は「２次関数を使って解く」ことがポイント！

このポイントをおさえていないと，応用問題が理解できなくなります！

この投稿を見れば，２次不等式の超基本はばっちり理解できます！

苦手な人にとってもわかりやすく解説しています！

　

２次関数を使った２次不等式の解き方

　２次関数 $y=x^2-x-2$ とおく

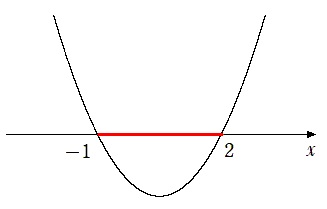
　２次不等式 $x^2-x-2<0$ を解くには

$y<0$ すなわち $x$ 軸より下側

　に２次関数がある $x$ の範囲を求める

　

　$y=0$ を代入すると

$x^2-x-2=0$

$(x+1)(x-2)=0$

$x=-1，2$

　$y<0$ を満たす $x$ の範囲を求めると

$-1<x<2$

　

　２次関数 $y=x^2-x-2$ とおく

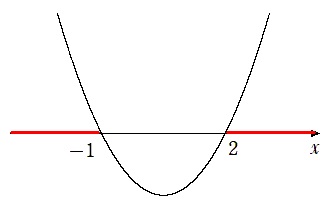
　２次不等式 $x^2-x-2<0$ を解くには

$y>0$ すなわち $x$ 軸より上側

　に２次関数がある $x$ の範囲を求める

　

　$y=0$ を代入すると

$x^2-x-2=0$

$(x+1)(x-2)=0$

$x=-1，2$

　$y>0$ を満たす $x$ の範囲を求めると

$x<-1，2<x$

　

２次不等式を解く

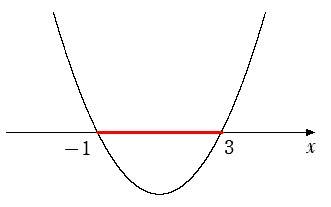
　(1)　$x^2-2x-3<0$

$(x+1)(x-3)<0$

$-1<x<3$

　

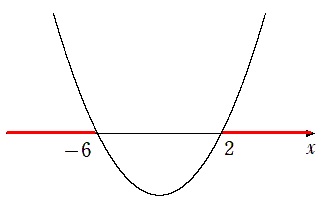
　(2)　$x^2+4x-12≧0$

$(x+6)(x-2)≧0$

$x≦-6，2≦x$

　

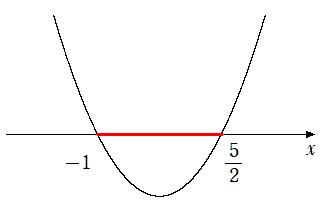
　(3)　$2x^2-3x-5<0$

$(x+1)(2x-5)<0$

$\displaystyle{x<-1，\frac{5}{2}<x}$

　

まとめ

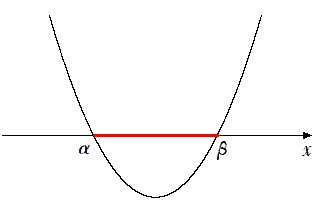
　$(x-α)(x-β)<0$ を解くと

$α<x<β$

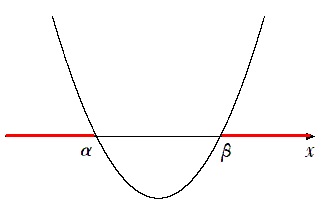
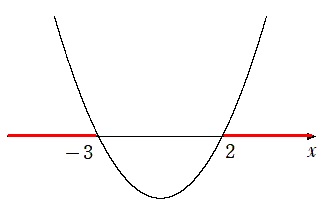
　$(x-α)(x-β)>0$ を解くと

$x<α，β<x$

問題

解答

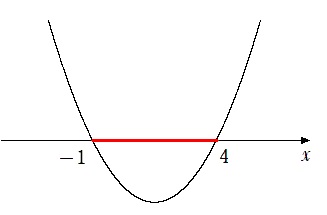
　(1)　$x^2-3x-4<0$

$(x+1)(x-4)<0$

$-1<x<4$

　

　(2)　$x^2+x-6≧0$

$(x+3)(x-2)≧0$

$x≦-3，2≦x$

　

　(3)　$2x^2-x-6<0$

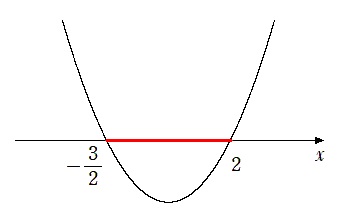
$(2x+3)(x-2)<0$

$\displaystyle{-\frac{3}{2}<x<2}$

　

　

🔰基本…まずはこの記事から！
🔵標準…基本問題や公式の理解度が重要！
🔴応用…場合分けなど思考力が要求される！