2次不等式のポイントは「2次関数を使って解く」こと!
そのときに2次関数とx軸の共有点を求める必要がある!
簡単な問題は因数分解して解けるが,中には因数分解できない問題も!
そんなときは2次方程式の解の公式を用いる!

因数分解ができないときの2次不等式の解き方がわからないよ…

因数分解ができないときは解の公式を使って解くことになるよ!
因数分解できるときの2次不等式の解き方
$(x-α)(x-β)<0$ を解くと
$α<x<β$
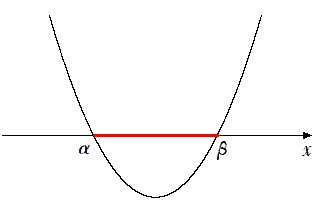
$(x-α)(x-β)>0$ を解くと
$x<α,β<x$
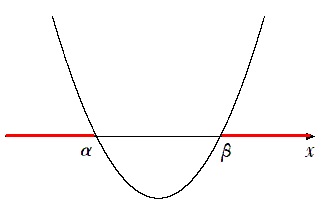
詳しい解き方は↓

因数分解できないときの2次不等式の解き方
2次関数 $y=x^2-x-1$ とおく
2次不等式 $x^2-x-1<0$ を解くには
$y<0$ すなわち $x$ 軸より下側
に2次関数がある $x$ の範囲を求める
$y=0$ を代入すると
$x^2-x-1=0$
$\displaystyle{x=\frac{1±\sqrt{5}}{2}}$ ←解の公式
$y<0$ を満たす $x$ の範囲を求めると
$\displaystyle{\frac{1-\sqrt{5}}{2}<x<\frac{1+\sqrt{5}}{2}}$
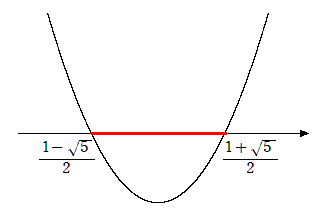
2次関数 $y=x^2-x-1$ とおく
2次不等式 $x^2-x-1>0$ を解くには
$y>0$ すなわち $x$ 軸より上側
に2次関数がある $x$ の範囲を求める
$y=0$ を代入すると
$x^2-x-1=0$
$\displaystyle{x=\frac{1±\sqrt{5}}{2}}$ ←解の公式
$y>0$ を満たす $x$ の範囲を求めると
$\displaystyle{x<\frac{1-\sqrt{5}}{2},\frac{1+\sqrt{5}}{2}<x}$
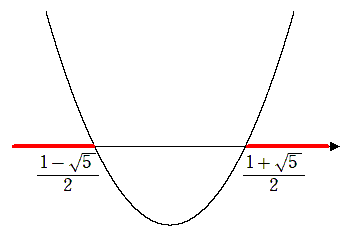

2次関数と $x$ 軸の共有点を求めるために解の公式を使うんだね!
まとめ
$ax^2+bx+c=0$ の実数解を $α,β$ とする
$ax^2+bx+c<0$ $(a>0)$ を解くと
$α<x<β$

$ax^2+bx+c>0$ $(a>0)$ を解くと
$x<α,β<x$

$ax^2+bx+c=0$ の実数解 $α,β$ は解の公式を用いると求まる
問題
問題 次の2次不等式を解け。
(1) $x^2-2x-2≦0$
(2) $x^2-x-3>0$
解答
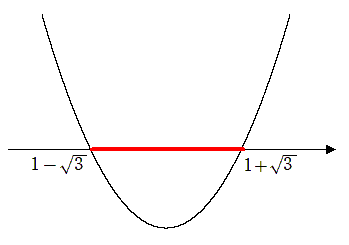
(1) $x^2-2x-2≦0$
$x^2-2x-2=0$ を解くと
$x=1±\sqrt{3}$
$1-\sqrt{3}≦x≦1+\sqrt{3}$
(2) $x^2-x-3>0$
$x^2-x-3=0$ を解くと
$\displaystyle{x=\frac{1±\sqrt{13}}{2}}$
$\displaystyle{x<\frac{1-\sqrt{13}}{2},\frac{1+\sqrt{13}}{2}<x}$

2次関数を使って2次不等式を解く場合は
2次関数と $x$ 軸の共有点が必要!
その共有点を求めるために解の公式を使うよ!
🔰平方完成|x²の係数が1以外の場合
🔰定義域における最大・最小
🔰基本形と一般形の利用
🔰2次方程式の解の公式
🔰2次方程式の実数解の個数と判別式
🔰2次関数のグラフとx軸の位置関係
🔰2次不等式|接する
🔰2次不等式|交わらない
🔰2次不等式|x²の係数が負
🔵絶対不等式
🔰基本…まずはこの記事から!
🔵標準…基本問題や公式の理解度が重要!
🔴応用…場合分けなど思考力が要求される!




コメント