x²の係数が負の数の場合の2次不等式はどうやって解く?
両辺にー1をかければ,基本的な2次不等式と同様に解くことができる!
しかし,間違えるポイントがあるので要注意!
不等式で負の数をかける場合は,『不等号の向きが変わる』!
このことに気を付ければばっちり!
2次不等式の解き方

2次不等式の解き方を復習するならこれ!


2次不等式のx²の係数が負の数の場合

$x^2$ の係数が負の数の場合どうやって解いたらいいのかな?
2次関数を使って考えてみよう!
$y=-x^2+x+2$ とおくと
$y=0$ を代入して
$-x^2+x+2=0$
$x^2-x-2=0$
$(x+1)(x-2)=0$
$x=-1,2$
2次不等式 $-x^2+x+2<0$ を解くには
$y<0$ すなわち $x$ 軸より下側
に2次関数がある $x$ の範囲を求める
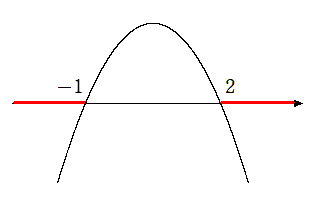
$y<0$ を満たす $x$ の範囲を求めると
$x<-1,2<x$

$x^2$ の係数が負の数の場合、2次関数が上に凸になるだけ!
あとは同じように解いたら解けるよ!

解けるのは分かったけど
下に凸になったり上に凸になったり
ミスしちゃいそう…

たしかにミスが増えそうだよね!
他の方法も考えてみよう!
両辺に $-1$ をかけて解く

両辺に $-1$ をかけて解くという方法もあるよ!
不等式で両辺に負の数をかけたりわったりするときに気を付けることは?

その通り!
その性質を用いて解いてみよう!
両辺に $-1$ をかけると
$x^2-x-2$$>$$0$
$(x+1)(x-2)>0$
$x<-1,2<x$
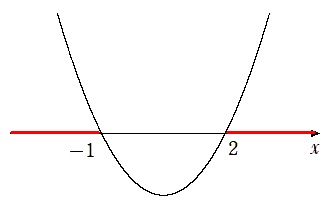

両辺に $-1$ をかけることで下に凸の2次関数で統一して考えることができるよ!
不等号の向きを変えることを忘れないようにしよう!
まとめ
2次不等式の $x^2$ の係数が負の数の場合
● 両辺に $-1$ をかける
● 不等号の向きを変えることを忘れない
問題
次の2次不等式を解け。
(1) $-x^2+x+2≧0$
(2) $-x^2+x+1<0$
解答
(1) $-x^2+x+2≧0$
両辺に $-1$ をかけると
$x^2-x-2$$≦$$0$
$(x+1)(x-2)≦0$
$-1≦x≦2$
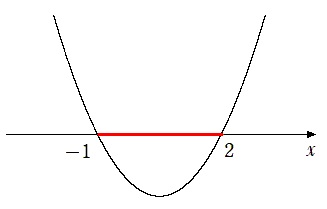
(2) $-x^2+x+1<0$
両辺に $-1$ をかけると
$x^2-x-1$$>$$0$
$x^2-x-1=0$ を解くと
$\displaystyle{x=\frac{1±\sqrt{5}}{2}}$
$\displaystyle{x<\frac{1-\sqrt{5}}{2},\frac{1+\sqrt{5}}{2}<x}$
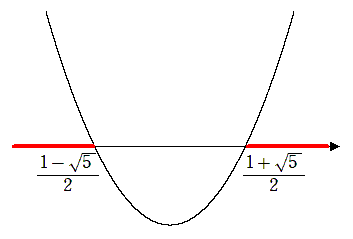

不等号の向きを変えることを忘れないように!
🔰平方完成|x²の係数が1以外の場合
🔰定義域における最大・最小
🔰基本形と一般形の利用
🔰2次方程式の実数解の個数と判別式
🔰2次関数のグラフとx軸の位置関係
🔰2次不等式|接する
🔰2次不等式|交わらない
🔵絶対不等式
🔰基本…まずはこの記事から!
🔵標準…基本問題や公式の理解度が重要!
🔴応用…場合分けなど思考力が要求される!





コメント