『2次関数の最大・最小』に関する問題は頻出です!
数学Ⅰの2次関数の分野だけでなく,他の分野の問題を解く際にも重要になります!
『2次関数の最大・最小』に関する問題の中でも苦手な人が多いのが,『場合分けが必要な問題』です!
この投稿では,場合分けが必要な問題の中でも
『定義域の両端に定数を含む(定義域の両端が動く)2次関数の最大・最小の問題』を解説します!
「2次関数の最大・最小の場合分けの問題が苦手」という人にオススメの投稿です!
これを見れば,『2次関数の最大・最小の場合分けの問題』はバッチリ!
問題
$f(x)=(x-2)^2+1$
軸は 直線 $x=2$,頂点 $(2,1)$
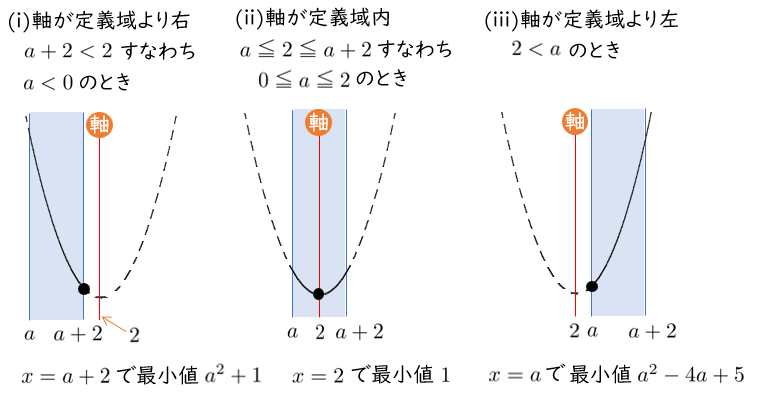
$a<0$ のとき $x=a+2$ で最小値 $a^2+1$
$0≦a≦2$ のとき $x=2$ で最小値 $1$
$2<a$ のとき $x=a$ で最小値 $a^2-4a+5$
$f(x)=(x-2)^2+1$
軸は 直線 $x=2$,頂点 $(2,1)$
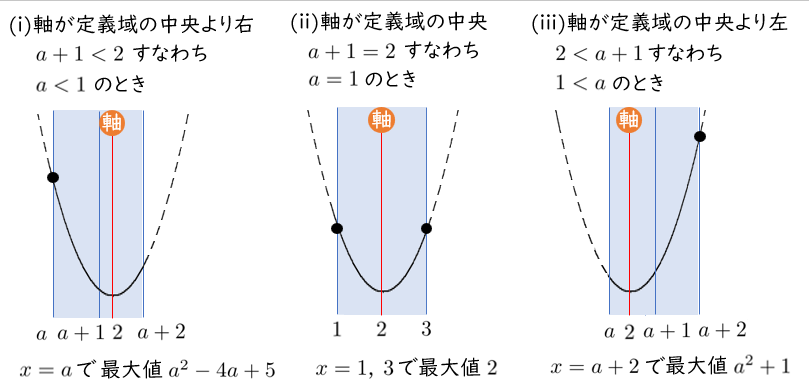
$a<1$ のとき $x=a$ で最大値 $a^2-4a+5$
$a=1$ のとき $x=1,3$ で最大値 $2$
$1<a$ のとき $a=a+2$ で最大値 $a^2+1$
『軸』や『定義域』の位置によって最大・最小が変わるので、場合分けを考える

2次関数の最大・最小の場合分けに関する問題のコツとポイントをまとめたよ!
2次関数の平方完成と軸・頂点
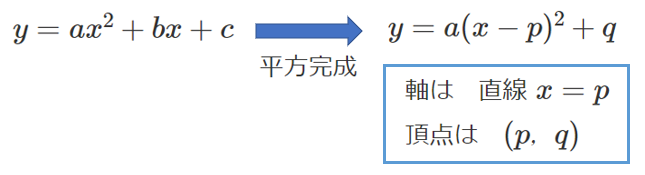
2次関数 $y=ax^2+bx+c$ を $y=a(x-p)^2+q$ に変形することを『平方完成』という。
平方完成して,$y=a(x-p)^2+q$ の形に変形することで,軸が直線 $x=p$,頂点が $(p,q)$ であることがわかる。
軸と頂点は,座標平面における2次関数の位置を表すので,『2次関数の最大・最小』の問題を解く際に重要です。

定義域における2次関数の最大・最小
定義域と値域
関数 $y=f(x)$ において
定義域 … 変数 $x$ のとりうる値の範囲
値域 … $x$ が定義域内のすべての値をとるときの $y$ のとりうる値の範囲
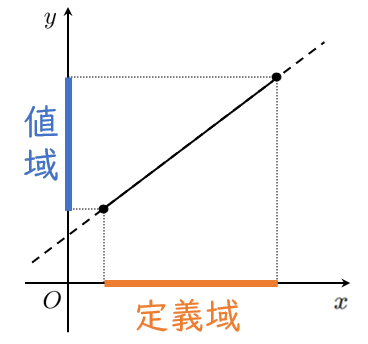
グラフを図示するとき,定義域内は実線,定義域外は点線で表すことが多い
定義域における2次関数の最大・最小
※定義域は関数の後ろに( )で付けられることが多い
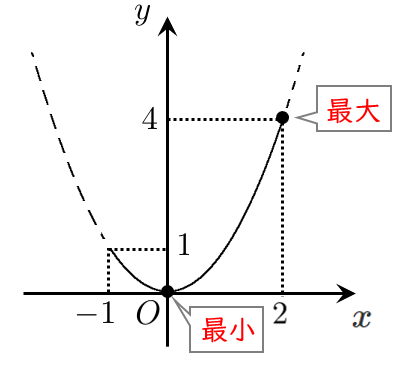
$x=2$ で最大値 $4$,$x=0$ で最小値 $0$
2次関数の最大・最小の問題を解くコツ
シンプルな図をかく

グラフが図示できれば,最大・最小は簡単に求まるね!

グラフをきちんとかけば確実に求まるけど,
もう少しシンプルな図を使って解く方法もあるよ!
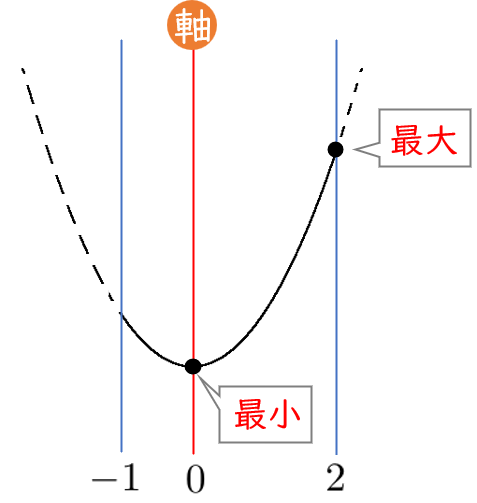

$x$ 軸や $y$ 軸をかいていないね!

最大と最小をとる位置がわかればいいから,
・グラフの形(下に凸か上に凸か)
・軸と定義域の位置関係
を図にすればOK!
最大・最小の候補
2次関数に最大値・最小値が存在するとすれば,『頂点』か『定義域の端点』のいずれかでとる。また,放物線は軸に関して対称である。
例えば,下に凸の放物線の場合,関数の値は
軸から遠くなるほど大きくなり,
軸から近くなるほど小さくなる。
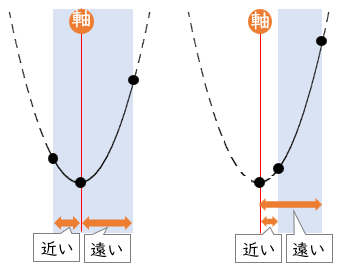
上に凸の場合はその逆となる。
・放物線は軸に関して対称
・軸と定義域の端点の距離を注意してグラフをかく
定義域の両端に定数を含むときの場合分け
最小値は、軸が定義域の右・内・左で場合分け
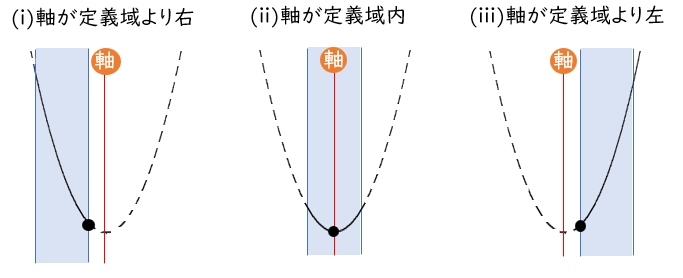
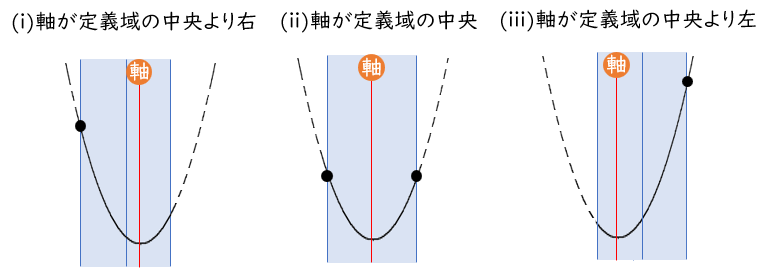
最大値は、軸が定義域の中央より右・中央・中央より左で場合分け
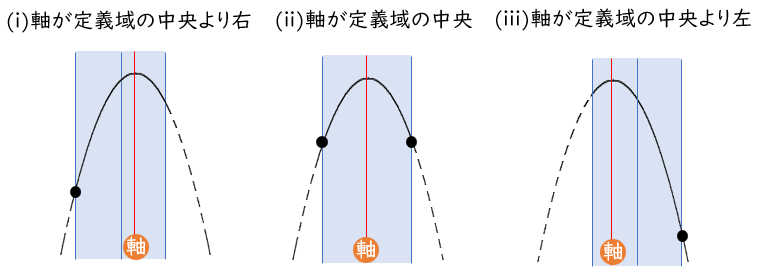
●上に凸の場合
最小値は、軸が定義域の中央より左・中央・中央より右で場合分け
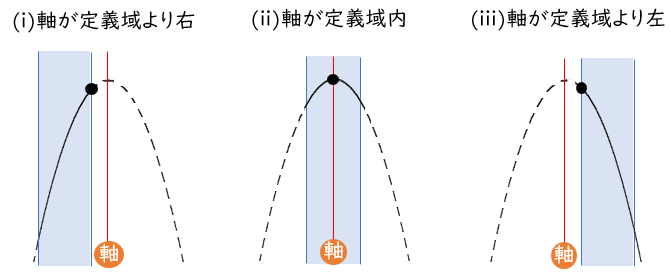
最大値は、軸が定義域の左・内・右で場合分け

下に凸の最小値と上に凸の最大値
下に凸の最大値と上に凸の最小値
の場合分けの考え方は同じだね!
復習
$f(x)=(x-2)^2+1$
軸は 直線 $x=2$,頂点 $(2,1)$

$a<0$ のとき $x=a+2$ で最小値 $a^2+1$
$0≦a≦2$ のとき $x=2$ で最小値 $1$
$2<a$ のとき $x=a$ で最小値 $a^2-4a+5$
$f(x)=(x-2)^2+1$
軸は 直線 $x=2$,頂点 $(2,1)$

$a<1$ のとき $x=a$ で最大値 $a^2-4a+5$
$a=1$ のとき $x=1,3$ で最大値 $2$
$1<a$ のとき $a=a+2$ で最大値 $a^2+1$
🔴軸に定数を含む2次関数の最大・最小の場合分け
🔴定義域の片端に定数を含む2次関数の最大・最小の場合分け
🔵因数分解形を利用した2次関数の決定
🔵2次関数のグラフと係数の符号
🔴場合分けが必要な文字係数の方程式
🔴文字係数の2次不等式
🔴異なる2つの正の解・負の解・異符号
🔴異なる2つの○より大きい・小さい解
🔰基本…まずはこの記事から!
🔵標準…基本問題や公式の理解度が重要!
🔴応用…場合分けなど思考力が要求される!




コメント