$n$ 進法から $10$ 進法はこれ↓

$10$ 進法から $n$ 進法はこれ↓


以上を駆使して,$n$ 進法を $m$ 進法で表せるようになろう!
n 進法を m 進法で表す

$2$ 進法の数を $3$ 進法で表したいときはどうする?

いきなりは難しそう!
$2$ 進法を $10$ 進法にしてから,$3$ 進法で表せばいいのかな?

その通り!
面倒くさいけど,その方法で確実に解こう!

問題を解いてみよう!
$110101_{(2)}=1\cdot2^5+1\cdot2^4+0\cdot2^3+1\cdot2^2+0\cdot2^1+1\cdot2^0$
$=32+16+0+4+0+1$
$=53$
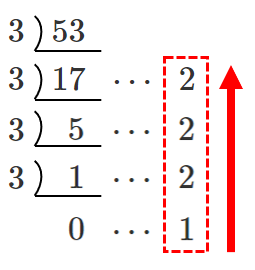
$53=1222_{(3)}$
よって, $110101_{(2)}=1222_{(3)}$
n 進法の四則演算

$n$ 進法の足し算や引き算の問題はどうやって解く?

そのまま $n$ 進法で計算するのは難しそう!
$10$ 進法で表して計算してから,$n$ 進法に戻せばいいのかな?

ちょっと遠回りだけど,その方が結果的にミスが少ないと思うよ!

問題を解いてみよう!
$110101_{(2)}=1\cdot2^5+1\cdot2^4+0\cdot2^3+1\cdot2^2+0\cdot2^1+1\cdot2^0$
$=32+16+0+4+0+1$
$=53$
$10101_{(2)}=1\cdot2^4+0\cdot2^3+1\cdot2^2+0\cdot2^1+1\cdot2^0$
$=16+0+4+0+1$
$=21$
$110101_{(2)}+10101{(2)}=53+21=74$
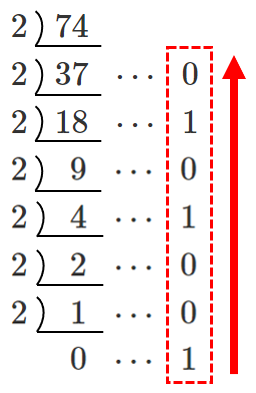
$74=1001010_{(2)}$
よって, $110101_{(2)}+10101{(2)}=1001010_{(2)}$

引き算や掛け算や割り算も,$10$ 進法にすれば計算できるね!
まとめ
● $n$ 進法を $m$ 進法で表す
$n$ 進法を $10$ 進法にして,$m$ 進法で表
● $n$ 進法の四則演算
$10$ 進法で表して計算してから $n$ 進法に戻す
問題
(2) $110101_{(2)}+10101{(2)}$ を計算せよ。
(1) $1222_{(3)}$ を $2$ 進法で表せ。
$1222_{(3)}=1\cdot3^3+2\cdot3^2+2\cdot3^1+2\cdot3^0$
$=27+18+6+2$
$=53$
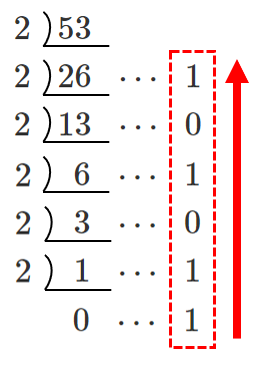
$53=110101_{(2)}$
よって, $1222_{(3)}=110101_{(2)}$
(2) $110101_{(2)}+10101{(2)}$ を計算せよ。
$110101_{(2)}=1\cdot2^5+1\cdot2^4+0\cdot2^3+1\cdot2^2+0\cdot2^1+1\cdot2^0$
$=32+16+0+4+0+1$
$=53$
$11111_{(2)}=1\cdot2^4+1\cdot2^3+1\cdot2^2+1\cdot2^1+1\cdot2^0$
$=16+8+4+2+1$
$=31$
$110101_{(2)}+11111{(2)}=53-31=22$
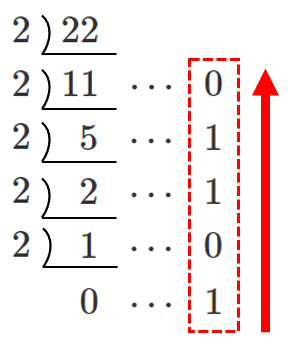
$22=10110_{(2)}$
よって, $110101_{(2)}+11111{(2)}=10110_{(2)}$

$10$ 進法を上手く使うことがポイント!




コメント