
$n$ 進法の基本はこれで復習しよう!
$n$ 進法の基本はこれ↓

10進法

普段使っている $10$ 進法について,詳しくみてみよう!
$2345$ は千の位を $2$,百の位を $3$,十の位を $4$,一の位を $5$ と考える

$2345=2\cdot10^3+3\cdot10^2+4\cdot10^1+5\cdot10^0$ ($10^0=1$)
- 位の取り方が $10^○$ の位
- 各位の数字が $0,1,2,\cdots,9$ の $10$ 種類
であるような表記方法を $10$ 進法という
10 進法の小数
$0.6789=6\cdot0.1+7\cdot0.01+8\cdot0.001+9\cdot0.0001$
$\displaystyle{=6\cdot\frac{1}{10^1}+7\cdot\frac{1}{10^2}+8\cdot\frac{1}{10^3}+9\cdot\frac{1}{10^4}}$
$10$ 進法では,小数点以下は $\displaystyle{\frac{1}{10^○}}$ の位である
2 進法の小数
$2$ 進法も,$10$ 進法と同様に考えることができる
n 進法の小数
$n$ 進法も $10$ 進法と同様に考えることができる
2 進法を 10 進法で表す
$\displaystyle{0.1011=1\cdot\frac{1}{2^1}+0\cdot\frac{1}{2^2}+1\cdot\frac{1}{2^3}+1\cdot\frac{1}{2^4}}$
$\displaystyle{=\frac{1}{2}+0+\frac{1}{8}+\frac{1}{16}}$
$\displaystyle{=\frac{11}{16}}$
$=0.6875$

位の考え方が分かれば解けるね!
10 進法を n 進法で表す
$10$ 進法の小数において,小数点以下は $\displaystyle{\frac{1}{10^○}}$ の位であるので,
$10$ をかけていくと,整数部分に各位の数が出てくる

$0.6789$ に $10$ をかけた $6.789$ の整数部分 $6$
$6.789$ の整数部分 $6$ を除いた $0.789$ に $10$ をかけた $7.89$ の整数部分 $7$
$7.89$ の整数部分 $7$ を除いた $0.89$ に $10$ をかけた $8.9$ の整数部分 $8$
$8.9$ の整数部分 $8$ を除いた $0.9$ に $10$ をかけた $9$
このように $10$ 進法の小数に $10$ をかけると,各位の数が求まる
10 進法の小数を 2 進法で表す

$10$ 進法の小数を $2$ 進法で表してみよう!
$2$ 進法の小数において,小数点以下は $\displaystyle{\frac{1}{2^○}}$ の位であるので,
$2$ をかけていくと,整数部分に各位の数が出てくる
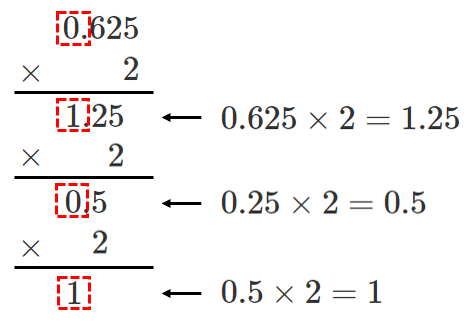
$0.625=0.101_{(2)}$
まとめ
● $n$ 進法の小数
$n$ 進法の小数点以下は $\displaystyle{\frac{1}{n^○}}$ の位
これを用いると,$n$ 進法の小数を $10$ 進法で表すことができる
● $10$ 進法の小数を $n$ 進法で表す
$n$ をかけて整数部分を取り出していく
問題
(2) $0.8125$ を $2$ 進法で表せ。
(1) $0.101_{(5)}$ を $10$ 進法で表せ。
$\displaystyle{0.101=1\times\frac{1}{5^1}+0\times\frac{1}{5^2}+1\times\frac{1}{5^3}}$
$\displaystyle{=\frac{1}{5}+0+\frac{1}{125}}$
$\displaystyle{=\frac{26}{125}}$
$=0.208$
(2) $0.8125$ を $2$ 進法で表せ。
$2$ 進法の小数において,小数点以下は $\frac{1}{2^○}$ の位であるので,
$2$ をかけていくと,整数部分に各位の数が出てくる
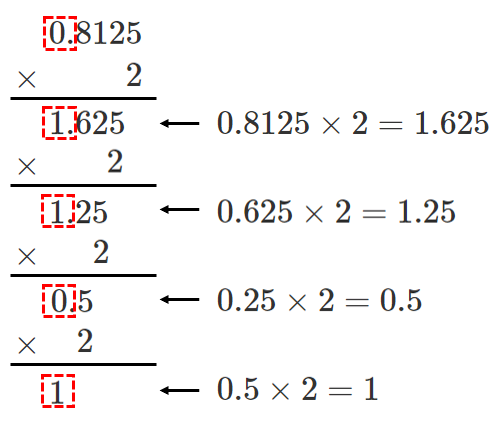
$0.8125=0.1101_{(2)}$

これで $n$ 進法はばっちり☆




コメント