
$\sqrt{A^2}$ を計算すると何になると思う?

$\sqrt{A^2}=A$
になると思うけど?

$\sqrt{A^2}=A$ という式は間違いなんだ!
間違える人がとても多いので要注意!
本当の式はこれ!
間違える人が多い公式の1つ『 √A²=|A| 』についてわかりやすく解説!
この公式の理解を深めて,周りの人と差をつけよう!
√A² の値
(1) $\sqrt{3^2}$
(2) $\sqrt{(-3)^2}$
(1) $\sqrt{3^2}=\sqrt{9}=3$
(2) $\sqrt{(-3)^2}=\sqrt{9}=3$

$\sqrt{(-3)^2}=-3$
という間違いがとても多いよ!

√の中に〇²ができたら,√がとれるって習ったけど…

そういう覚え方をすると間違えてしまうので気を付けよう!
$\sqrt{(-3)^2}=-3$
左辺は正,右辺は負になってるから,この式は間違いだよ!
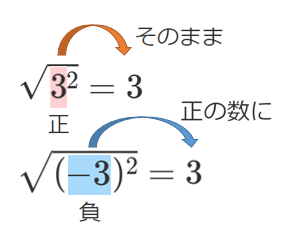

$\sqrt{A^2}$ は $A$ に正の数を入れても,負の数を入れても,計算結果は必ず正の数になる!

何を入れても計算結果が必ず正になるって…
絶対値と似ているね!
√A² と絶対値の関係

先ほどの $\sqrt{A^2}$ の計算と絶対値のはずし方を見比べてみよう!
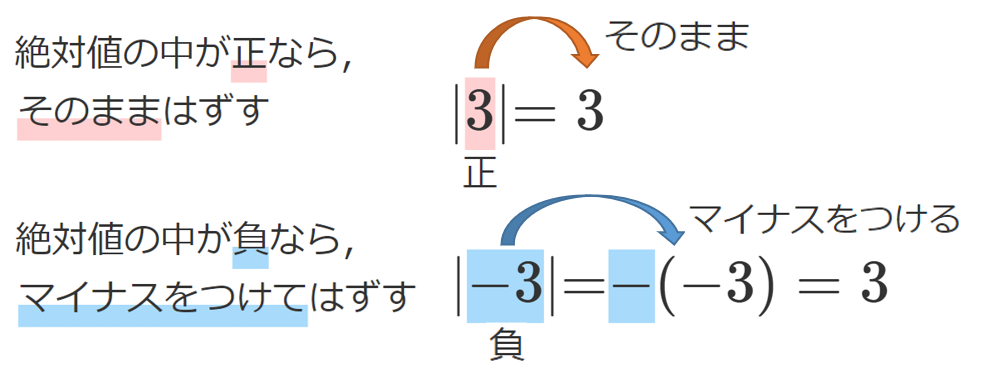
絶対値の復習はこれ↓

$\sqrt{A^2}$ と絶対値 $|A|$ はどちらも
$A$ に正の数を入れればそのまま
$A$ に負の数を入れれば正の数になる
という同じ性質をもつ!
だから,次の式が成り立つよ!

$\sqrt{A^2}$ は絶対値をつけて考えるってことだね!
問題演習
(1) $\sqrt{(1-\sqrt{2})^2}$
(2) $a>0$,$b<0$ のとき,$\sqrt{a^2b^2}$
(1) $1-\sqrt{2}<0$ より,
\begin{eqnarray} \sqrt{(1-\sqrt{2})^2} & = & |1-\sqrt{2}| \\ & = & -(1-\sqrt{2}) \\ & = & \sqrt{2}-1 \end{eqnarray}$1-\sqrt{2}$ は負なので,マイナスをつけて絶対値をはずす
(2) $a>0$,$b<0$ より,$ab<0$
\begin{eqnarray} \sqrt{a^2b^2} & = & \sqrt{(ab)^2} \\ & = & |ab| \\ & = & -ab \end{eqnarray}$ab$ は負なので,マイナスをつけて絶対値をはずす
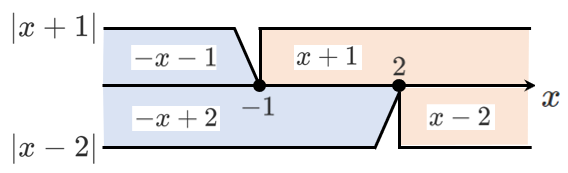
$x < -1$ のとき
$|x+1|=-x-1$,$|x-2|=-x+2$ なので
$-1 ≦ x < 2$ のとき
$|x+1|=x+1$,$|x-2|=-x+2$ なので
$2 ≦ x$ のとき
$|x+1|=x+1$,$|x-2|=x-2$ なので
まとめると
\begin{align} &|x+1|+|x-2|=\left\{ \begin{array}{lll} -2x+1 (x<-1 のとき) \\ 3 (-1 ≦ x < 2 のとき) \\ 2x-1 (2≦x のとき) \end{array} \right. \end{align}したがって
\begin{align} &\sqrt{x^2+2x+1}+\sqrt{x^2-4x+4}=\left\{ \begin{array}{lll} -2x+1 (x<-1 のとき) \\ 3 (-1 ≦ x < 2 のとき) \\ 2x-1 (2≦x のとき) \end{array} \right. \end{align}
絶対値が2つの場合分けはこれで学べる↓


$\sqrt{A^2}=|A|$ を確実に覚えておこう!
🔰基本…まずはこの記事から!
🔵標準…基本問題や公式の理解度が重要!
🔴応用…場合分けなど思考力が要求される!





コメント