高校数学Ⅰの『図形と計量』で習う『正弦定理』や『余弦定理』を用いて、空間図形を考える問題を解説しました!
空間図形の問題を解くためのポイントは、「三角形に着目して考える」こと!
空間図形の問題は、平面図形を駆使して考えることが重要です!
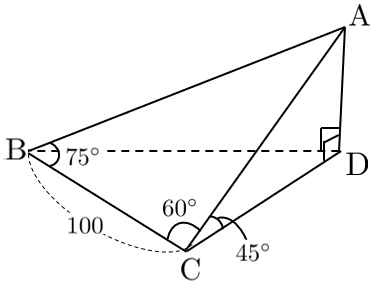
右図において、$\textrm{BC}=100$、$\angle\textrm{ABC}=75^\circ$、$\angle\textrm{ACB}=60^\circ$、$\angle\textrm{ACD}=45^\circ$ のとき、$\textrm{AD}$ の長さを求めよ。
<空間図形の問題は、三角形に着目して考える>
・長さや角度について情報がある $\triangle\textrm{ABC}$ と $\triangle\textrm{ACD}$ に着目して考えていく。
・$\triangle\textrm{ACD}$ について、$\textrm{AC}$ の長さがわかれば $\textrm{AD}$ の長さが求まる。
($\triangle\textrm{ACD}$ は直角二等辺三角形だから)
・$\triangle\textrm{ABC}$ について、『正弦定理』や『余弦定理』を用いれば、$\textrm{AC}$ の長さが求まりそう。
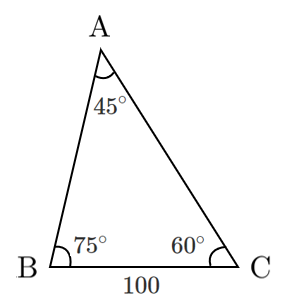
まずは $\triangle\textrm{ABC}$ で正弦定理を用いて $\textrm{AB}$ の長さを求める
※辺 $\textrm{AC}$ の対角が $75^\circ$ なので、いきなり $\textrm{AC}$ の長さは求まらない
$\triangle\textrm{ABC}$ で正弦定理より
$\displaystyle{\frac{100}{\sin45^\circ}=\frac{\textrm{AB}}{\sin60^\circ}}$
これを解いて $\textrm{AB}=50\sqrt{6}$
$\textrm{AB}$ の長さが求まったので、余弦定理で $\textrm{AC}$ の長さが求まる
$\textrm{AC}=x$ として、$\triangle\textrm{ABC}$ で余弦定理より
$(50\sqrt{6})^2=x^2+100^2-2\cdot x\cdot100\cos60^\circ$
$x^2-100x-5000=0$
$x>0$ より $x=50+50\sqrt{3}$
$\textrm{AC}$ が求まったので、直角二等辺三角形 $\textrm{ACD}$ で $\textrm{AD}$ が求まる
$\triangle\textrm{ACD}$ について
\begin{eqnarray} \textrm{AD} &=& \textrm{AC}\sin45^\circ \\ &=& \frac{50\sqrt{3}+50}{\sqrt{2}} \\ &=& 25\sqrt{6}+25\sqrt{2} \\ &=& 25(\sqrt{6}+\sqrt{2}) \end{eqnarray}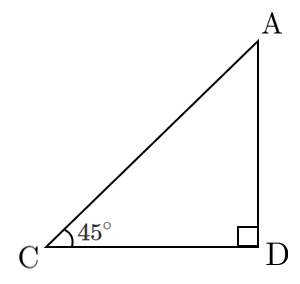




コメント