中学数学や高校数学Ⅰで、「1次方程式」や「2次方程式」「絶対値を含む方程式」など、様々な方程式を習いました。
高校数学Ⅰの図形と計量では、三角比 $\sin\theta$、$\cos\theta$、$\tan\theta$ を含む方程式が登場します。
「三角比を含む方程式」は、『単位円を利用すること』がポイントです!
この記事では、「三角比を含む方程式」の解き方をわかりやすく解説しました!
問題
(1) $\displaystyle{\sin\theta=\frac{1}{2}}$ (2) $\displaystyle{\sin\theta=\frac{1}{\sqrt{2}}}$ (3) $\displaystyle{\sin\theta=\frac{\sqrt{3}}{2}}$
(4) $\displaystyle{\cos\theta=\frac{\sqrt{3}}{2}}$ (5) $\displaystyle{\cos\theta=-\frac{1}{2}}$ (6) $\displaystyle{\cos\theta=-\frac{1}{\sqrt{2}}}$
(7) $\displaystyle{\tan\theta=\sqrt{3}}$ (8) $\displaystyle{\tan\theta=-\frac{1}{\sqrt{3}}}$ (9) $\displaystyle{\tan\theta=-1}$
(1) $\theta=30^\circ,150^\circ$ (2) $\theta=45^\circ,135^\circ$ (3) $\theta=60^\circ,120^\circ$
(4) $\theta=30^\circ$ (5) $\theta=120^\circ$ (6) $\theta=135^\circ$
(7) $\theta=60^\circ$ (8) $\theta=150^\circ$ (9) $\theta=135^\circ$
三角比に関する方程式とは
という問題のように、$\sin\theta$ の値が $\displaystyle{\frac{1}{2}}$ であるような角 $\theta$ の値を求める問題のことを「三角比を含む方程式」といいます。
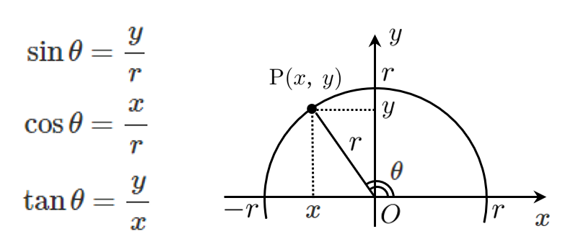
三角比の定義
単位円の利用
単位円とは『半径1の円』のことです。
三角比の定義について、$r=1$ とすると $\sin$ と $\cos$ の式がシンプルに表すことができます。
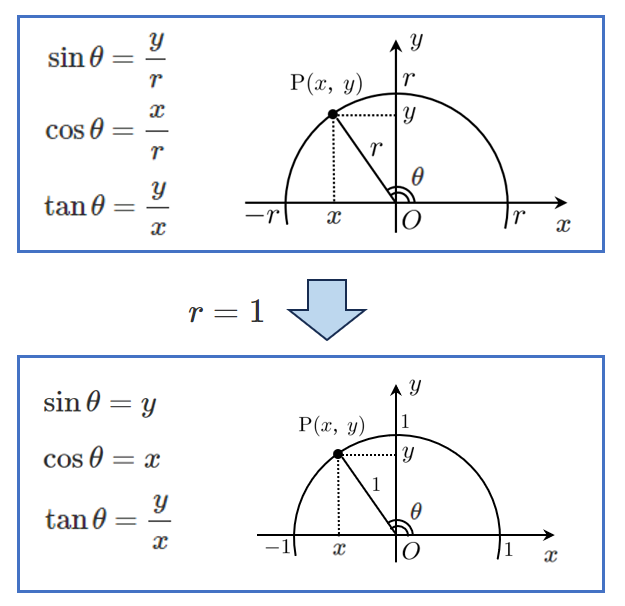
単位円($r=1$)で考えると
$\sin\theta=y$ すなわち $\sin\theta$ は $y$ 座標
$\cos\theta=y$ すなわち $\cos\theta$ は $x$ 座標
と考えることができます。
$r=1$ としても、$\displaystyle{\tan\theta=\frac{y}{x}}$ であり、定義式は変わりません。
斜辺の長さが1である30°,45°,60°の直角三角形
斜辺の長さ ( $r$ ) を $1$ で固定した $30^\circ$、$45^\circ$、$60^\circ$ の直角三角形を考えると、
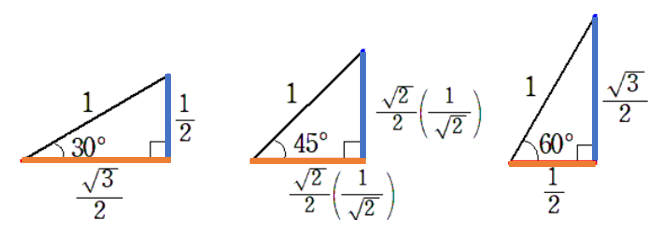
この直角三角形を単位円上に当てはめてみると、以下のような図ができる。
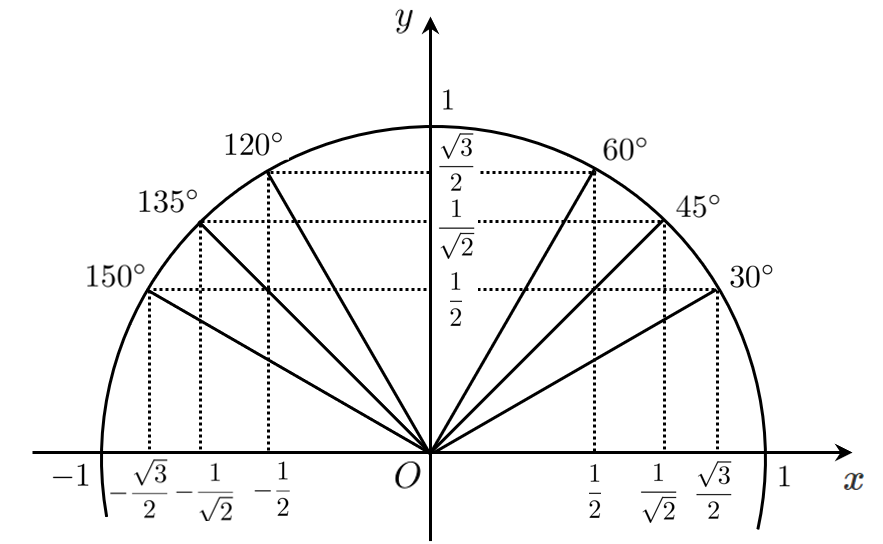
単位円($r=1$)で考えると
$\sin\theta=y$ すなわち $\sin\theta$ は $y$ 座標
$\cos\theta=y$ すなわち $\cos\theta$ は $x$ 座標
と考えることができるので、上の図を用いると以下の表を作ることができます。
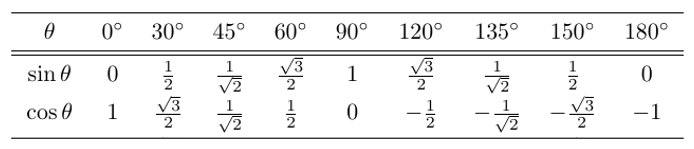
単位円を用いると、座標を読み取るだけで $\sin$ と $\cos$ の値がわかります。
$\sin$ を含む方程式
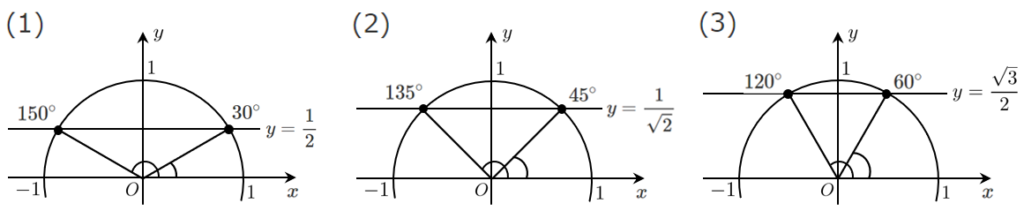
単位円において、$\sin\theta=y$ すなわち $\sin\theta$ は $y$ 座標 であることを利用すると、単位円に直線 $y=○$ を引くことで角 $\theta$ を求めることができます。
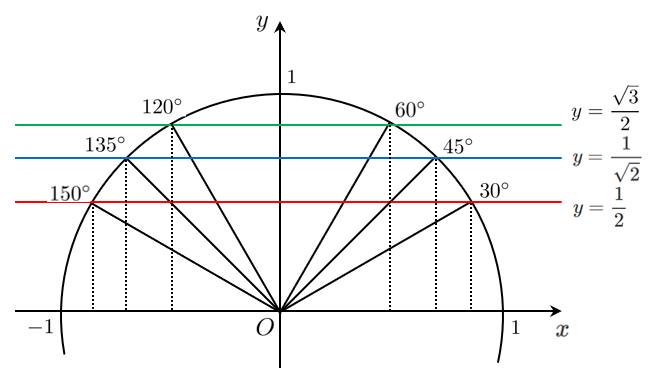
図のような3本の直線のどれかを引くことで、角 $\theta$ を求めることができます。
ちなみに、$\displaystyle{\frac{1}{2}<\frac{\sqrt{2}}{2}<\frac{\sqrt{3}}{2}}$ という大小関係になります。$\displaystyle{\left(\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}\right)}$
$\displaystyle{y=\frac{1}{2}}$ は $0$ と $1$ の真ん中に引く ➡ $30^\circ$ または $150^\circ$
$\displaystyle{y=\frac{\sqrt{3}}{2}}$ は $1$ の近くに引く ➡ $60^\circ$ または $120^\circ$
$\displaystyle{y=\frac{1}{\sqrt{2}}}$ は $\displaystyle{\frac{1}{2}}$ と $\displaystyle{\frac{\sqrt{3}}{2}}$ の間に引く ➡ $45^\circ$ または $135^\circ$
($\displaystyle{\frac{1}{\sqrt{2}}}$ は $45^\circ$ の直角三角形なので、$45^\circ$ と $135^\circ$ に関係がある)
(1) $\displaystyle{\sin\theta=\frac{1}{2}}$ (2) $\displaystyle{\sin\theta=\frac{1}{\sqrt{2}}}$ (3) $\displaystyle{\sin\theta=\frac{\sqrt{3}}{2}}$
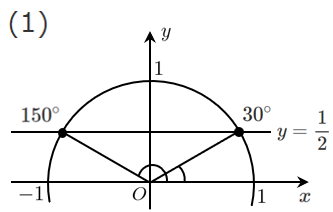
(1) $\displaystyle{\sin\theta=\frac{1}{2}}$
$\theta=30^\circ,150^\circ$
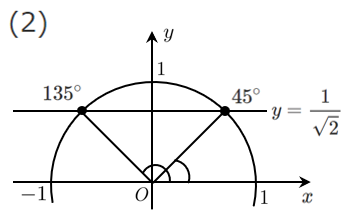
(2) $\displaystyle{\sin\theta=\frac{1}{\sqrt{2}}}$
$\theta=45^\circ,135^\circ$
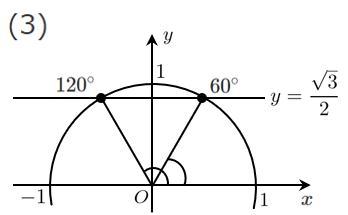
(3) $\displaystyle{\sin\theta=\frac{\sqrt{3}}{2}}$
$\theta=60^\circ,150^\circ$
$\cos$ を含む方程式
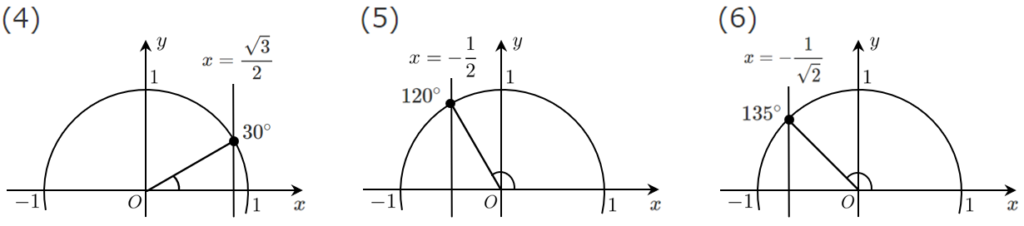
単位円において、$\cos\theta=y$ すなわち $\cos\theta$ は $x$ 座標 であることを利用すると、単位円に直線 $x=○$ を引くことで角 $\theta$ を求めることができます。
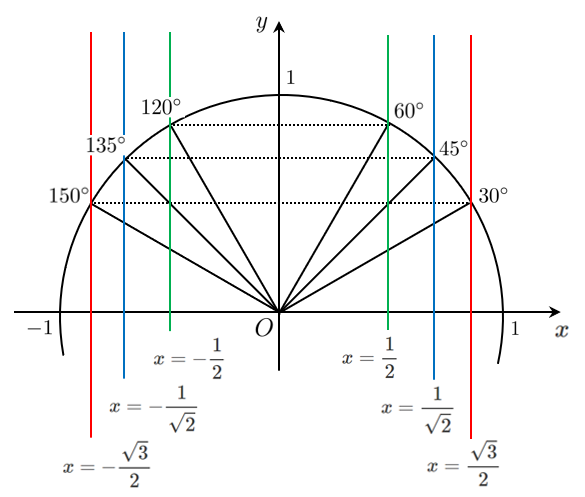
図のような6本の直線のどれかを引くことで、角 $\theta$ を求めることができます。
ちなみに、$\displaystyle{\frac{1}{2}<\frac{\sqrt{2}}{2}<\frac{\sqrt{3}}{2}}$ という大小関係になります。$\displaystyle{\left(\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}\right)}$
$\displaystyle{x=\frac{1}{2}}$ は $0$ と $1$ の真ん中に引く ➡ $60^\circ$
$\displaystyle{x=-\frac{1}{2}}$ は $0$ と $-1$ の真ん中に引く ➡ $120^\circ$
$\displaystyle{y=\frac{\sqrt{3}}{2}}$ は $1$ の近くに引く ➡ $30^\circ$
$\displaystyle{y=\frac{-\sqrt{3}}{2}}$ は $-1$ の近くに引く ➡ $150^\circ$
$\displaystyle{y=\frac{1}{\sqrt{2}}}$ は $\displaystyle{\frac{1}{2}}$ と $\displaystyle{\frac{\sqrt{3}}{2}}$ の間に引く ➡ $45^\circ$
$\displaystyle{y=-\frac{1}{\sqrt{2}}}$ は $\displaystyle{-\frac{1}{2}}$ と $\displaystyle{-\frac{\sqrt{3}}{2}}$ の間に引く ➡ $135^\circ$
($\displaystyle{\frac{1}{\sqrt{2}}}$ は $45^\circ$ の直角三角形なので、$45^\circ$ と $135^\circ$ に関係がある)
(4) $\displaystyle{\cos\theta=\frac{\sqrt{3}}{2}}$ (5) $\displaystyle{\cos\theta=-\frac{1}{2}}$ (6) $\displaystyle{\cos\theta=-\frac{1}{\sqrt{2}}}$
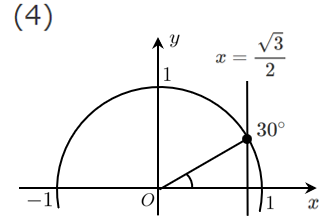
(4) $\displaystyle{\cos\theta=\frac{\sqrt{3}}{2}}$
$\theta=30^\circ$
(5) $\displaystyle{\sin\theta=\frac{1}{\sqrt{2}}}$
$\theta=120^\circ$
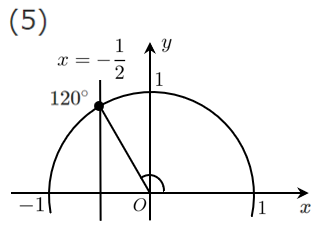
(6) $\displaystyle{\sin\theta=\frac{\sqrt{3}}{2}}$
$\theta=135^\circ$
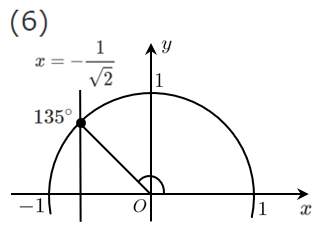
$tan$ を含む方程式
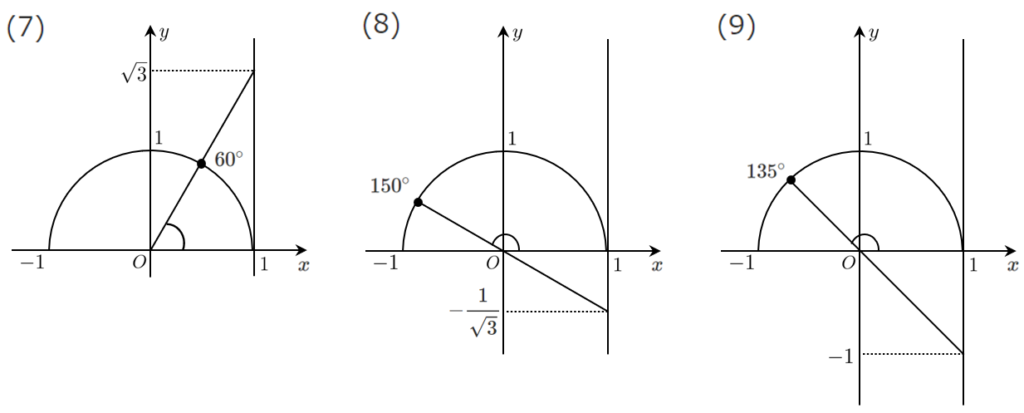
$\tan$ は $\displaystyle{\frac{y}{x}}$ より、『傾き』を表しており、『直線 $x=1$ との交点の $y$ 座標』が $\tan\theta$ と考えることができる。($x=1$ で固定すると $y$ 座標が $\tan\theta$)
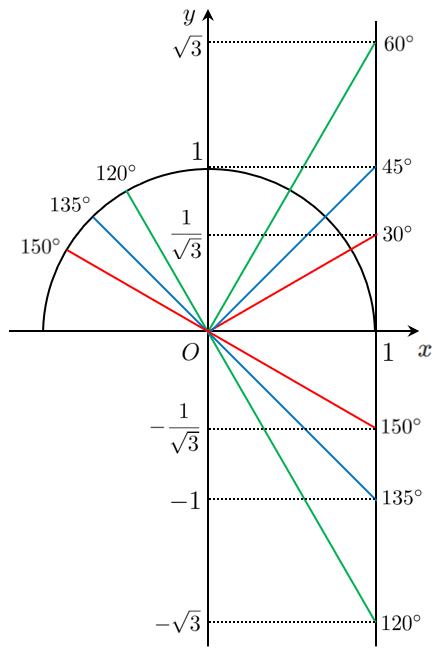
図のような6本の直線のどれかを引くことで、角 $\theta$ を求めることができます。
極端な話をすると、
$\displaystyle{\frac{1}{\sqrt{3}}}$ と $\displaystyle{-\frac{1}{\sqrt{3}}}$ は傾きが緩やか
$1$ と $-1$ は傾きが普通
$\sqrt{3}$ と $-\sqrt{3}$ は傾きが急
と考えることができます。
$\displaystyle{\frac{1}{\sqrt{3}}}$ と $\displaystyle{-\frac{1}{\sqrt{3}}}$ は傾きが緩やか ➡ それぞれ $30^\circ$ と $150^\circ$
$1$ と $-1$ は傾きが普通 ➡ それぞれ $45^\circ$ と $135^\circ$
$\sqrt{3}$ と $-\sqrt{3}$ は傾きが急 ➡ それぞれ $60^\circ$ と $120^\circ$
(7) $\displaystyle{\tan\theta=\sqrt{3}}$ (8) $\displaystyle{\tan\theta=-\frac{1}{\sqrt{3}}}$ (9) $\displaystyle{\tan\theta=-1}$
(7) $\displaystyle{\tan\theta=\sqrt{3}}$
$\theta=60^\circ$
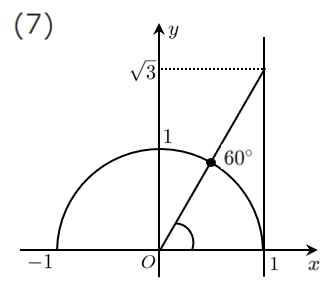
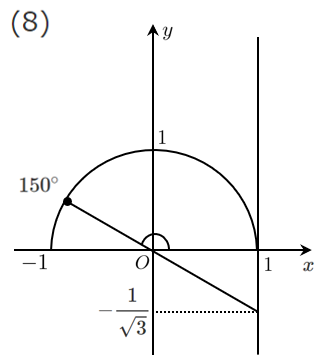
(8) $\displaystyle{\tan\theta=-\frac{1}{\sqrt{3}}}$
$\theta=150^\circ$
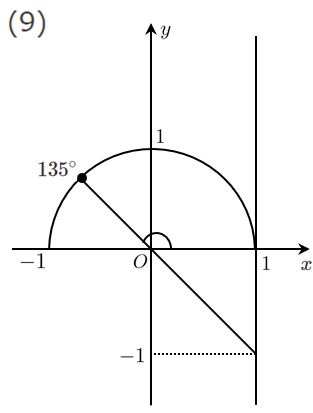
(9) $\displaystyle{\tan\theta=-1}$
$\theta=135^\circ$
まとめ
● $\sin$ を含む方程式

● $\cos$ を含む方程式

● $\tan$ を含む方程式





コメント