余弦定理の使い方を整理しよう！式は図とセットで覚えるのがコツ！

数学Ⅰ「図形と計量」分野で最も登場機会が多いと言っても過言ではない『余弦定理』

『余弦定理』の式は図とセットで覚えるのがコツです！

辺の長さを求める式と，cosの値を求める式を使いこなせるようにしましょう！

この投稿を見れば，『余弦定理』はばっちり！

余弦定理
余弦定理で辺の長さを求める
余弦定理で角（$\cos$ の値）を求める
余弦定理の証明
まとめ

余弦定理

余弦定理

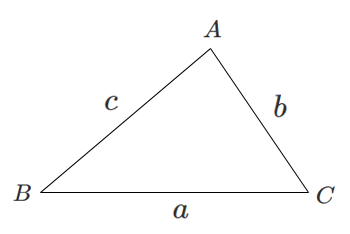
　$\triangle ABC$ において

$$a^2=b^2+c^2-2bc\cos A$$

$$b^2=c^2+a^2-2ca\cos B$$

$$c^2=a^2+b^2-2ab\cos C$$

式は３つとも覚える必要はないよ！

下図のように覚えよう！

$■^2=○^2+□^2-2○□\cos\theta$

ポイント

　余弦定理は，２辺（○と□）とその間の角（$\theta$）の $\cos$ で残りの辺（■）が求まる定理

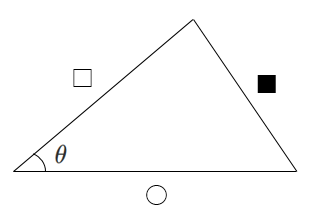
$\cos$ の値に自信がない人はこれ↓

三角比の拡張

鈍角の三角比の考え方きちんと理解していますか？鋭角の三角比は直角三角形で考えていましたが，鈍角の三角比は座標で考えるので少し難しく感じます！ですが，基本をきちんとおさえることで必ず理解できます！単位円を使った鈍角の三角比の考え方をわかりやすく解説します！

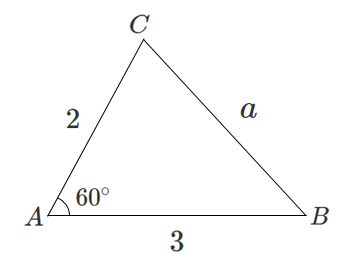
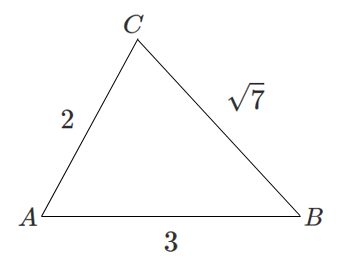
余弦定理で辺の長さを求める

　$\triangle ABC$ において，$b=2$，$c=3$，$A=60^\circ$ のとき，$a$ を求めよ。

余弦定理より \begin{eqnarray} a^2 &=& 2^2+3^2-2・2・3・\cos60^\circ \\\\ &=& 4+9-2・2・3・\frac{1}{2} \\\\ &=& 7 \end{eqnarray}

　$a>0$ より　　$a=\sqrt{7}$

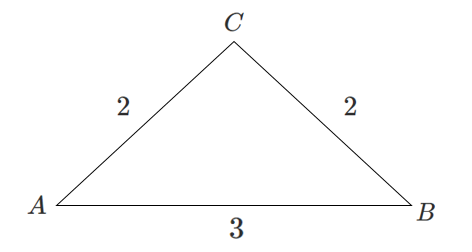
余弦定理で角（$\cos$ の値）を求める

余弦定理 $a^2=b^2+c^2-2bc\cos A$ を変形する

$$2bc\cos A=b^2+c^2-a^2$$

$$\displaystyle\cos A=\frac{b^2+c^2-a^2}{2bc}$$

角（$\cos$ の値）を求めたいときはこの式を使えばいいんだね！

$\displaystyle{\cos\theta=\frac{○^2+□^2-■^2}{2○□}}$

ポイント

　３辺の長さがわかっていれば，角（$\cos$ の値）を求めることができる

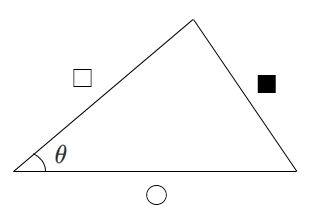
実際に問題を解いてみよう！

　$\triangle ABC$ において，$a=\sqrt{7}$，$b=2$，$c=3$ のとき，$A$ を求めよ。

余弦定理より \begin{eqnarray} \cos A &=& \frac{2^2+3^2-(\sqrt{7})^2}{2・2・3} \\\\ &=& \frac{4+9-7}{2・2・3} \\\\ &=& \frac{6}{2・2・3} \\\\ &=& \frac{6}{2・2・3} \\\\ &=& \frac{1}{2} \end{eqnarray}

　$0^\circ<A<180^\circ$ より　$A=60^\circ$

$\triangle ABC$ において，$a=2$，$b=2$，$c=3$ のとき，$\cos C$ を求めよ。

余弦定理より \begin{eqnarray} \cos A &=& \frac{2^2+2^2-3^2}{2・2・2} \\\\ &=& \frac{4+4-9}{2・2・2} \\\\ &=& \frac{-1}{2・2・2} \\\\ &=& -\frac{1}{8} \end{eqnarray}

余弦定理の証明

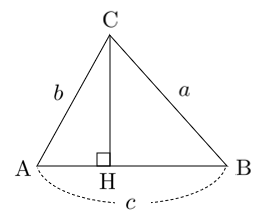
$a^2=b^2+c^2-2bc\cos A$ を $\angle A$ が鋭角・鈍角で分けて考える。

（ア）$\textrm{A}<90^\circ$ のとき

　　$\textrm{CH}=b\sin A$

　　$\textrm{BH}=c-b\cos A$

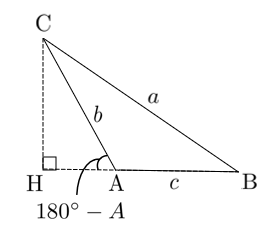
（イ）$\textrm{A}>90^\circ$ のとき

　　$\textrm{CH}=b\sin(180^\circ-A)=b\sin A$

　　$\textrm{BH}=c+b\cos(180^\circ-A)=c-b\cos A$

（ア）,（イ）いずれの場合でも

\begin{eqnarray} a^2 &=& \textrm{CH}^2+\textrm{BH}^2 \\ &=& (b\sin A)^2+(c-b\cos A)^2 \\ &=& b^2(\sin^2A+\cos^2A)+c^2-2bc\cos A \\ &=& b^2+c^2-2bc\cos A \end{eqnarray}