高校数学Ⅰの『図形と計量』の定着度がはかれる重要問題の1つである『円に内接する四角形の対角線と面積』に関する問題を解説しました!
余弦定理、180°-θの公式、面積の公式といった『図形と計量』で登場する公式の理解度の確認ができます!
問題
四角形 $\textrm{ABCD}$ は円に内接しており、$\textrm{AB}=2$、$\textrm{BC}=2$、$\textrm{CD}=3$、$\textrm{DA}=4$ である。このとき、対角線 $\textrm{BD}$ の長さと四角形 $\textrm{ABCD}$ の面積 $S$ を求めよ。
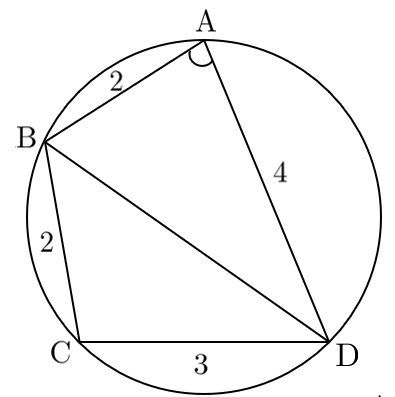
$\triangle\textrm{ABD}$ で余弦定理より
\begin{eqnarray} \textrm{BD}^2 &=& 2^2+4^2-2・2・4・\cos A \\ &=& 20-16\cos A \cdots ①\\ \end{eqnarray}$\triangle\textrm{BCD}$ で余弦定理より
\begin{eqnarray} \textrm{BD}^2 &=& 2^2+3^2-2・2・3・\cos(180^\circ-A) \\ &=& 13-12\cdot(-\cos A) \\ &=& 13+12\cos A \cdots ② \\ \end{eqnarray}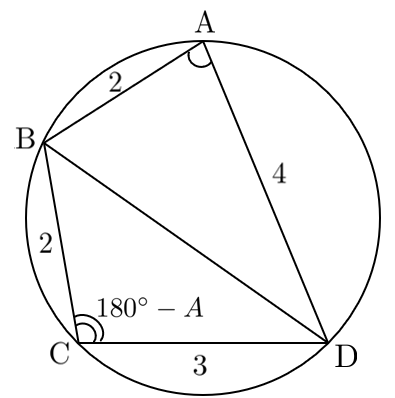
①、②より、$\textrm{BD}^2$ を消去して
\begin{eqnarray} 20-16\cos A &=& 13+12\cos A \\ \cos A &=& \frac{1}{4} \\ \end{eqnarray}①に代入して $\displaystyle{\textrm{BD}^2=20-16\cdot\frac{1}{4}=16}$
$\textrm{BD}>0$ より $\textrm{BD}=4$
$\sin^2 A+\cos^2 A=1$,$\sin A>0$ より
$\displaystyle{\sin A=\sqrt{1-\left(\frac{1}{4}\right)^2}=\frac{\sqrt{15}}{4}}$
よって、四角形の面積 $S$ は
\begin{eqnarray} S &=& \triangle\textrm{ABD}+\triangle\textrm{BCD} \\ &=& \frac{1}{2}\cdot2\cdot4\sin A+\frac{1}{2}\cdot2\cdot3\sin(180^\circ-A) \\ &=& 4\sin A+3\sin A \\ &=& 7\sin A \\ &=& \frac{7\sqrt{15}}{4} \\ \end{eqnarray}円に内接する四角形のポイント
『円に内接する四角形の対角の和は $180^\circ$ である』という性質と、
$\cos(180^\circ-\theta)=\cos\theta$ や $\sin(180^\circ-\theta)=\sin\theta$
を用いて、円に内接する四角形の対角線の長さや面積を求めることができる
円に内接する四角形の性質
円に内接する四角形の対角の和は $180^\circ$
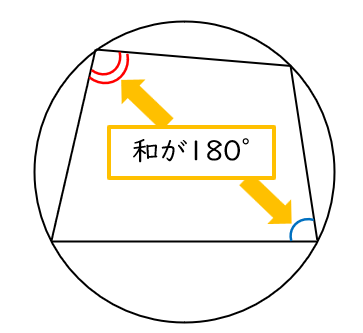
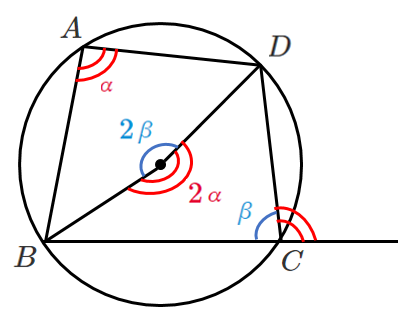
<証明>
四角形 $\textrm{ABCD}$ が円に接するとき
$\angle \textrm{BAD}=α$,$\angle \textrm{BCD}=β$ とする
円周角と中心角の関係より
$2α+2β=360°$
となるから $α+β=180°$
また $\angle \textrm{BCD}$ の外角は $180°-β=α$ となる
180°-θの公式
$\sin(180^\circ-\theta)=\sin\theta$(足して $ 180^\circ$ の $\sin$ は同じ)
$\cos(180^\circ-\theta)=-\cos\theta$(足して $ 180^\circ$ の $\cos$ は異符号)
$\tan(180^\circ-\theta)=-\tan\theta$(足して $ 90^\circ$ の $\tan$ は異符号)
問題解説
四角形 $\textrm{ABCD}$ は円に内接しており、$\textrm{AB}=2$、$\textrm{BC}=2$、$\textrm{CD}=3$、$\textrm{DA}=4$ である。このとき、対角線 $\textrm{BD}$ の長さと四角形 $\textrm{ABCD}$ の面積 $S$ を求めよ。

- 対角線 $\textrm{BD}$ で分けられた2つの三角形($\triangle\textrm{ABD}$ と $\triangle\textrm{BCD}$)において余弦定理を用いて、$\textrm{BD}^2$ を2通りで表す。
- 『$180^\circ-\theta$ の公式』を利用して、$\cos(180^\circ-A)=-\cos A$ とする。
- $\textrm{BD}^2$ を消去して、$\cos A$ を求める。
- 1.の余弦定理の式に $\cos A$ の値を代入して $\textrm{BD}$ を求める。
$\triangle\textrm{ABD}$ で余弦定理より
\begin{eqnarray} \textrm{BD}^2 &=& 2^2+4^2-2・2・4・\cos A \\ &=& 20-16\cos A \cdots ①\\ \end{eqnarray}$\triangle\textrm{BCD}$ で余弦定理より
\begin{eqnarray} \textrm{BD}^2 &=& 2^2+3^2-2・2・3・\cos(180^\circ-A) \\ &=& 13-12\cdot(-\cos A) \\ &=& 13+12\cos A \cdots ② \\ \end{eqnarray}
①、②より、$\textrm{BD}^2$ を消去して
\begin{eqnarray} 20-16\cos A &=& 13+12\cos A \\ \cos A &=& \frac{1}{4} \\ \end{eqnarray}①に代入して $\displaystyle{\textrm{BD}^2=20-16\cdot\frac{1}{4}=16}$
$\textrm{BD}>0$ より $\textrm{BD}=4$
- $\cos A$ から $\sin A$ を求める。
- 2つの三角形($\triangle\textrm{ABD}$ と $\triangle\textrm{BCD}$)の和で面積 $S$ を考える。
- $\sin(180^\circ-A)=\sin A$ を用いて、面積 $S$ を求める。
$\sin^2 A+\cos^2 A=1$,$\sin A>0$ より
$\displaystyle{\sin A=\sqrt{1-\left(\frac{1}{4}\right)^2}=\frac{\sqrt{15}}{4}}$
よって、四角形の面積 $S$ は
\begin{eqnarray} S &=& \triangle\textrm{ABD}+\triangle\textrm{BCD} \\ &=& \frac{1}{2}\cdot2\cdot4\sin A+\frac{1}{2}\cdot2\cdot3\sin(180^\circ-A) \\ &=& 4\sin A+3\sin A \\ &=& 7\sin A \\ &=& \frac{7\sqrt{15}}{4} \\ \end{eqnarray}




コメント