高校数学Ⅰの『図形と計量』で学ぶ『正四面体の体積の求め方』についてわかりやすく解説しました!
空間図形の基本の定着はもちろん、平面図形でよく使われる定理の復習にもなります!
この投稿を読んで、『正四面体の体積の求め方』をマスターしましょう!
問題
正四面体の体積は $\displaystyle{\frac{1}{3}\times(底面積)\times(高さ)}$ で求まる
1辺の長さが $a$ である正四面体 $\textrm{OABC}$ の体積は
$\displaystyle{\frac{1}{3}\times(\triangle\textrm{ABC}の面積)\times(高さ \textrm{OH})}$
$\triangle\textrm{ABC}$ は正三角形なので面積は
$\displaystyle{\frac{1}{2}\cdot a\cdot a \sin60^\circ=\frac{\sqrt{3}}{4}a^2}$
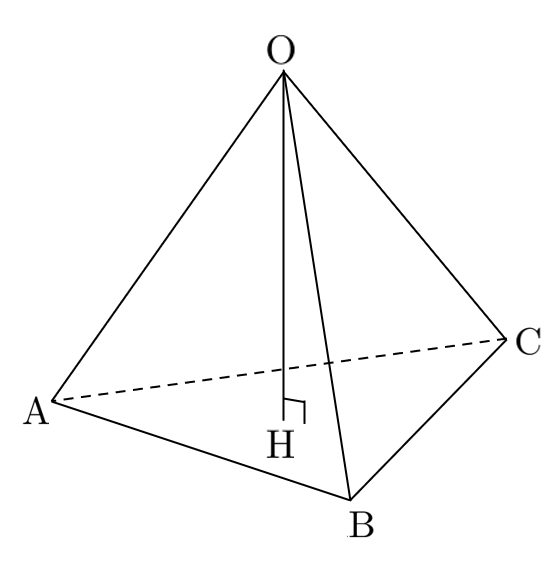
$\triangle\textrm{OAH}$、$\triangle\textrm{OBH}$、$\triangle\textrm{OCH}$ は直角三角形であり、斜辺と他の1辺 $\textrm{OH}$ の長さが等しいので合同である。
$\textrm{AH}=\textrm{BH}=\textrm{CH}$ が成り立つため、点 $\textrm{H}$ は$\triangle\textrm{ABC}$ の外心である。
よって、 $\textrm{AH}$ は $\triangle\textrm{ABC}$ の外接円の半径と等しい。
$\triangle\textrm{ABC}$ で正弦定理より
\begin{eqnarray} 2\textrm{AH} &=& \frac{a}{\sin60^\circ} \\ \textrm{AH} &=& \frac{1}{\sqrt{3}}a \end{eqnarray}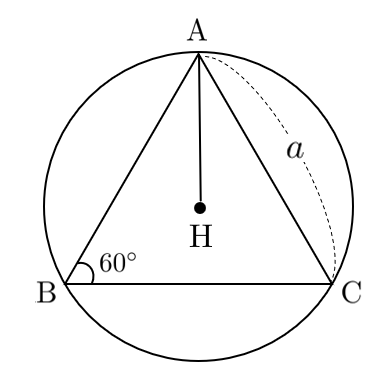
$\triangle\textrm{OAH}$ で三平方の定理より
\begin{eqnarray} \textrm{OH} &=& \sqrt{a^2-\left(\frac{1}{\sqrt{3}}a\right)^2} \\ &=& \frac{\sqrt{2}}{\sqrt{3}}a \\ &=& \frac{\sqrt{6}}{3}a \end{eqnarray}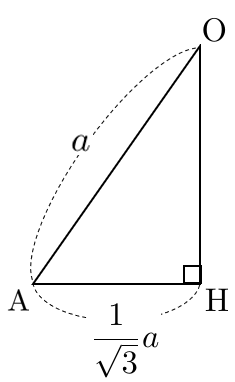
したがって、1辺の長さが $a$ である正四面体の体積は
$\displaystyle{\frac{1}{3}\cdot\frac{\sqrt{3}}{4}a^2\cdot\frac{\sqrt{6}}{3}a=\frac{\sqrt{2}}{12}}$
※ $\triangle\textrm{ABC}$ は正三角形なので、点 $\textrm{H}$ は $\triangle\textrm{ABC}$ の外心、内心、重心である。
(別解)高さ $\textrm{OH}$ 求め方
『点 $\textrm{H}$ が $\triangle\textrm{ABC}$ の重心であることを利用する』
辺 $\textrm{BC}$ の中点 $\textrm{M}$ とすると
$\displaystyle{\textrm{OM}=\textrm{AM}=\frac{\sqrt{3}}{2}}$
点 $\textrm{H}$ は $\triangle\textrm{ABC}$ の重心なので
$\textrm{AH}:\textrm{AM}=2:1$
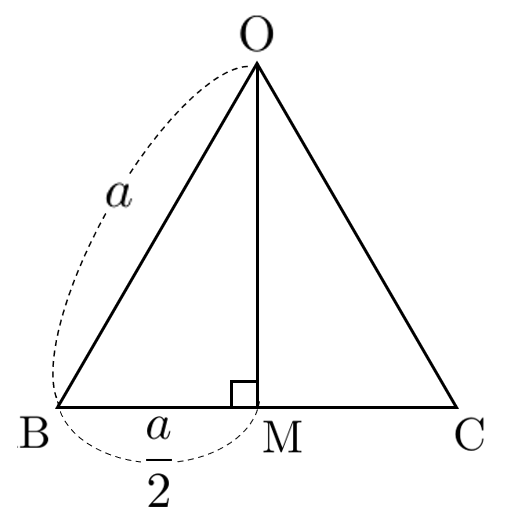
$\triangle\textrm{OMH}$ において
$\displaystyle{\cos\angle\textrm{OMH}=\frac{\textrm{HM}}{\textrm{OM}}=\frac{\frac{1}{3}\textrm{AM}}{\textrm{AM}}=\frac{1}{3}}$
よって
$\displaystyle{\sin\angle\textrm{OMH}=\sqrt{1-(\cos\angle\textrm{OMH})^2}=\frac{2\sqrt{2}}{3}}$
以上より
\begin{eqnarray} \textrm{OH} &=& \textrm{OM}\sin\angle\textrm{OMH} \\ &=& \frac{\sqrt{3}}{2}a\times\frac{2\sqrt{2}}{3} \\ &=& \frac{\sqrt{6}}{3}a \end{eqnarray}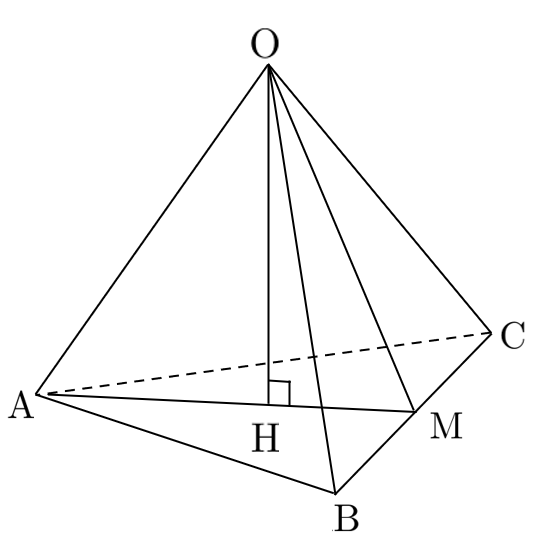
正四面体とは
正四面体とは、4つの合同な正三角形を面とする四面体である。
すべての面は正三角形なので、すべての辺の長さが等しい。
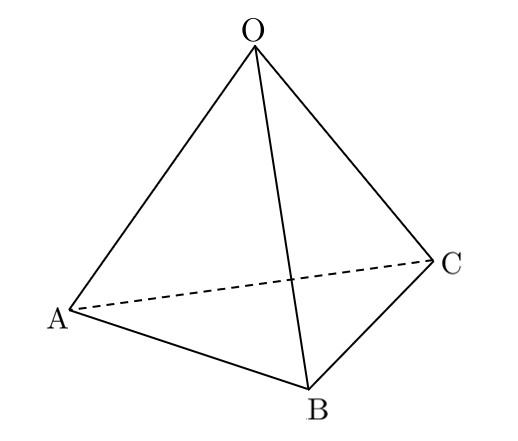
正四面体の体積の求め方
頂点 $\textrm{O}$ から面 $\textrm{ABC}$ に垂線 $\textrm{OH}$ を下ろすと、正四面体の体積 $V$ は
$\displaystyle{V=\frac{1}{3}\times(底面\textrm{ABC})\times(高さ \textrm{OH})}$
で求めることができる。
底面である $\triangle\textrm{ABC}$ の面積と高さ $\textrm{OH}$ の長さを求めることで、正四面体の体積は求まる。

底面である△ABCの求め方
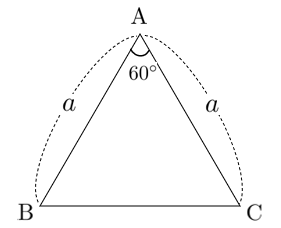
$\triangle\textrm{ABC}$ は正三角形なので面積は
$\displaystyle{\frac{1}{2}\cdot a\cdot a \sin60^\circ=\frac{\sqrt{3}}{4}a^2}$
高さOHの求め方
点Hは△ABCの外心・内心・重心
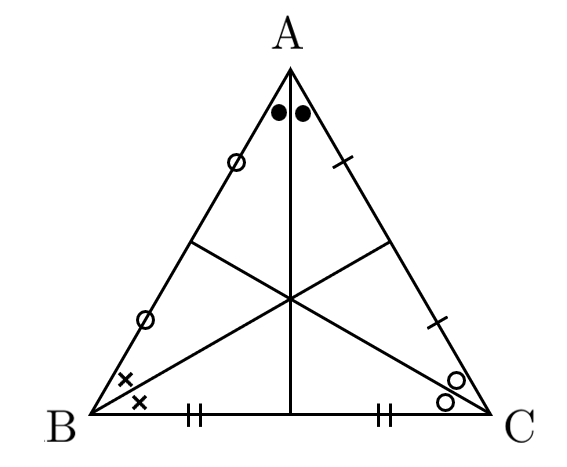
頂点 $\textrm{O}$ から $\triangle\textrm{ABC}$ に垂線 $\textrm{OH}$ を下ろしたとき、点 $\textrm{H}$ は $\triangle\textrm{ABC}$ の外心・内心・重心である。
●外心
辺の垂直二等分線の交点
外接円の中心
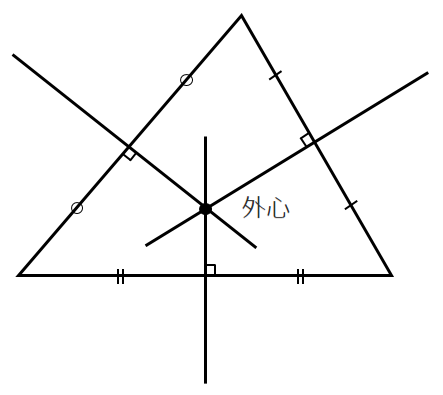
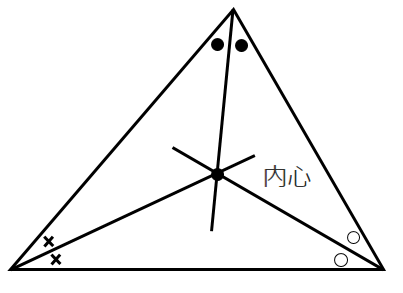
●内心
角の二等分線の交点
内接円の中心
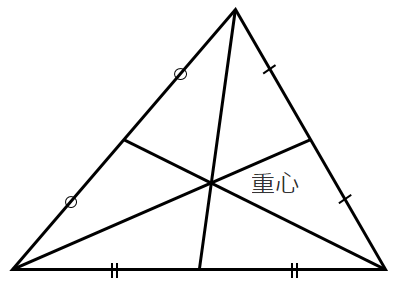
●重心
中線(頂点と対辺の中点を結ぶ線)の交点
$\triangle\textrm{OAH}$、$\triangle\textrm{OBH}$、$\triangle\textrm{OCH}$ は直角三角形であり、斜辺と他の1辺 $\textrm{OH}$ の長さが等しいので合同である。
よって、$\textrm{AH}=\textrm{BH}=\textrm{CH}$ が成り立つため、点 $\textrm{H}$ は$\triangle\textrm{ABC}$ の外心である。

正三角形において、辺の垂直二等分線と角の二等分線と中線は一致するので、
正三角形の外心と内心と重心は一致する。
よって、$\triangle\textrm{ABC}$ は正三角形なので、
$\triangle\textrm{ABC}$ の外心と内心と重心は一致する。
点Hが外心であることを利用して高さOHを求める
点 $\textrm{H}$ は $\triangle\textrm{ABC}$ の外心なので、$\textrm{AH}$ は $\triangle\textrm{ABC}$ の外接円の半径と等しい。
$\triangle\textrm{ABC}$ で正弦定理より
\begin{eqnarray} 2\textrm{AH} &=& \frac{a}{\sin60^\circ} \\ \textrm{AH} &=& \frac{1}{\sqrt{3}}a \end{eqnarray}
$\triangle\textrm{OAH}$ で三平方の定理より
\begin{eqnarray} \textrm{OH} &=& \sqrt{a^2-\left(\frac{1}{\sqrt{3}}a\right)^2} \\ &=& \frac{\sqrt{2}}{\sqrt{3}}a \\ &=& \frac{\sqrt{6}}{3}a \end{eqnarray}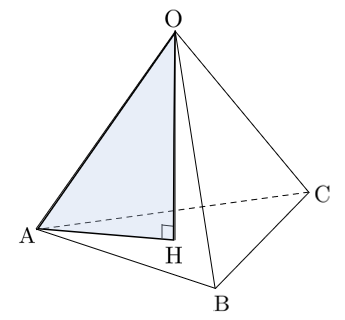

点Hが重心であることを利用して高さOHを求める
辺 $\textrm{BC}$ の中点 $\textrm{M}$ とすると
$\displaystyle{\textrm{OM}=\textrm{AM}=\frac{\sqrt{3}}{2}}$
点 $\textrm{H}$ は $\triangle\textrm{ABC}$ の重心なので
$\textrm{AH}:\textrm{AM}=2:1$

$\triangle\textrm{OMH}$ において
$\displaystyle{\cos\angle\textrm{OMH}=\frac{\textrm{HM}}{\textrm{OM}}=\frac{\frac{1}{3}\textrm{AM}}{\textrm{AM}}=\frac{1}{3}}$
よって
$\displaystyle{\sin\angle\textrm{OMH}=\sqrt{1-(\cos\angle\textrm{OMH})^2}=\frac{2\sqrt{2}}{3}}$
以上より
\begin{eqnarray} \textrm{OH} &=& \textrm{OM}\sin\angle\textrm{OMH} \\ &=& \frac{\sqrt{3}}{2}a\times\frac{2\sqrt{2}}{3} \\ &=& \frac{\sqrt{6}}{3}a \end{eqnarray}
正四面体の体積
$\triangle\textrm{ABC}$ の面積は $\displaystyle{\frac{\sqrt{3}}{4}a^2}$
高さ $\textrm{OH}$ は $\displaystyle{\frac{\sqrt{6}}{3}a}$

したがって、四面体の体積 $V$は
\begin{eqnarray} V &=& \frac{1}{3}\times(底面\textrm{ABC})\times(高さ\textrm{OH}) \\ &=& \frac{1}{3}\times\frac{\sqrt{3}}{4}a^2\times\frac{\sqrt{6}}{3}a \\ &=& \frac{\sqrt{2}}{12}a^3 \end{eqnarray}1辺の長さが $a$ である正四面体の高さと体積
1辺の長さが $a$ である正四面体の
高さは $\displaystyle{\frac{\sqrt{6}}{3}a}$ 体積は $\displaystyle{\frac{\sqrt{2}}{12}a^3}$





コメント