90°-θの三角比の公式覚えていますか?
忘れがちな三角比の公式の一つです!
式が複雑そうに見えるのが覚えにくい理由として挙げられます!
式だけ見るのではなく,式の意味を理解することが大切です!
この投稿を見れば,90°-θの公式をもう忘れません!

まずは三角比の定義の復習をしよう!
詳しく学びたい人は↓

三角比の定義
直角三角形の鋭角($90^\circ$ 未満の角)の1つを $\theta$ とし,斜辺の長さを $r$ ,その他の辺の長さを下図のように $x$,$y$ とするとき,三角比の定義は以下のようになる。
※ $x$ のことを $\theta$ の隣の辺なので「隣辺」,$y$ のことを $\theta$ の向かいの辺なので「対辺」とよぶこともある。
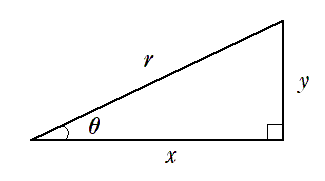
$\displaystyle{\sin\theta=\frac{y}{r}}$, $\displaystyle{\cos\theta=\frac{x}{r}}$, $\displaystyle{\tan\theta=\frac{y}{x}}$
● $\sin\theta$ の覚え方
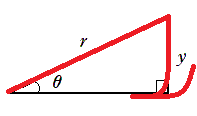
$s$ の筆記体で $\displaystyle{\sin\theta=\frac{y}{r}}$
● $\cos\theta$ の覚え方
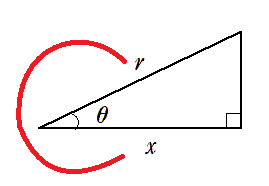
$c$ と書いて $\displaystyle{\cos\theta=\frac{x}{r}}$
● $\tan\theta$ の覚え方
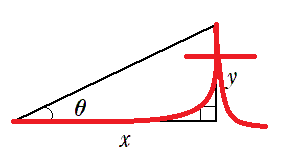
$t$ の筆記体で $\displaystyle{\tan\theta=\frac{y}{x}}$
90°-θ の三角比
直角三角形の一方の角を $\theta$ とすると,
他方の角は $ 90^\circ-\theta$ と表せる
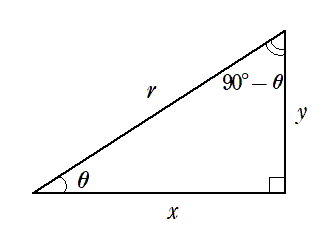
この図において $\displaystyle{\sin\theta=\frac{y}{r}}$,$ \displaystyle{ \cos\theta=\frac{x}{r}}$,$ \displaystyle{ \tan\theta=\frac{y}{x}}$ である
直角三角形を回転させると
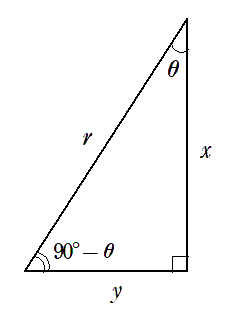
この図において,三角比を考えると
$$\sin(90^\circ-\theta)=\frac{x}{r}$$
$$\cos(90^\circ-\theta)=\frac{y}{r}$$
$$\tan(90^\circ-\theta)=\frac{x}{y}$$
となる
$ \displaystyle{ \sin\theta=\frac{y}{r}}$,$ \displaystyle{ \cos\theta=\frac{x}{r}}$,$ \displaystyle{ \tan\theta=\frac{y}{x}}$ より
$$\sin(90^\circ-\theta)=\cos\theta$$
$$\cos(90^\circ-\theta)=\sin\theta$$
$$\tan(90^\circ-\theta)=\frac{1}{\tan\theta}$$

この式は見たことあるんだけど,すぐに忘れちゃうんだよね…

この式で覚えようとしない方がいいよ!
90°-θ の三角比の覚え方
$●+■=90^\circ$ とすると
$\sin●=\cos■$(足して $ 90^\circ$ の $\sin$ と $\cos$ は同じ)
$\tan●=\frac{1}{\tan■}$(足して $ 90^\circ$ の $\tan$ は逆数の関係)

こんな感じで覚えておこう!
90°-θ の具体例
30°,45°,60° の三角比を具体例に $ 90^\circ-\theta$ を見てみる
| $\theta$ | 30$^\circ$ | 45$^\circ$ | 60$^\circ$ |
| $\sin\theta$ | $\frac{1}{2}$ | $\frac{1}{\sqrt{2}}$ | $\frac{\sqrt{3}}{2}$ |
| $\cos\theta$ | $\frac{\sqrt{3}}{2}$ | $\frac{1}{\sqrt{2}}$ | $\frac{1}{2}$ |
| $\tan\theta$ | $\frac{1}{\sqrt{3}}$ | $1$ | $\sqrt{3}$ |
$$\sin30^\circ=\cos60^\circ$$
$$\sin45^\circ=\cos45^\circ$$
$$\sin60^\circ=\cos30^\circ$$
足して $ 90^\circ$ の $\sin$ と $\cos$ は同じ
$$\tan30^\circ=\frac{1}{\tan60^\circ}$$
$$\tan45^\circ=\frac{1}{\tan45^\circ}$$
$$\tan60^\circ=\frac{1}{\tan30^\circ}$$
足して $ 90^\circ$ の $\tan$ は逆数の関係
まとめ
● $ 90^\circ-\theta$ の三角比
$\sin(90^\circ-\theta)=\cos\theta$
$\cos(90^\circ-\theta)=\sin\theta$
$\displaystyle{\tan(90^\circ-\theta)=\frac{1}{\tan\theta}}$
● $ 90^\circ-\theta$ の三角比の覚え方
$●+■=90^\circ$ とすると
$\sin●=\cos■$(足して $ 90^\circ$ の $\sin$ と $\cos$ は同じ)
$\displaystyle{\tan●=\frac{1}{\tan■}}$(足して $ 90^\circ$ の $\tan$ は逆数の関係)
● $ 90^\circ-\theta$ の三角比を用いると $ 45^\circ$ 以下の三角比で表すことができる
例 $\sin60^\circ=\cos30^\circ$
$\cos60^\circ=\sin30^\circ$
$\displaystyle{\tan60^\circ=\frac{1}{\tan30^\circ}}$
問題
次の三角比を $ 45^\circ$ 以下の三角比で表せ。
(1) $\sin70^\circ$
(2) $\cos55^\circ$
(3) $\tan64^\circ$
解答
(1) $\sin70^\circ=\cos20^\circ$
足して $ 90^\circ$ の $\sin$ と $\cos$ は同じ
(2) $\cos55^\circ=\sin35^\circ$
足して $ 90^\circ$ の $\sin$ と $\cos$ は同じ
(3) $\displaystyle{\tan64^\circ=\frac{1}{\tan26^\circ}}$
足して $ 90^\circ$ の $\tan$ は逆数の関係

$ 90^\circ-\theta$ の三角比は忘れやすいので要注意!




コメント