高校数学Ⅰの『図形と計量』で重要問題の1つである『三角形の角の二等分線の長さ』に関する問題をわかりやすく解説しました!
『角度が与えられている場合』と『角度が与えられていない場合』の2種類の問題を解けるようにしましょう!
問題
(1) $\textrm{AB}=3$,$\textrm{AC}=5$,$\angle\textrm{A}=120^\circ$ の $\triangle\textrm{ABC}$ において,角の二等分線 $\textrm{AD}$ の長さを求めよ。
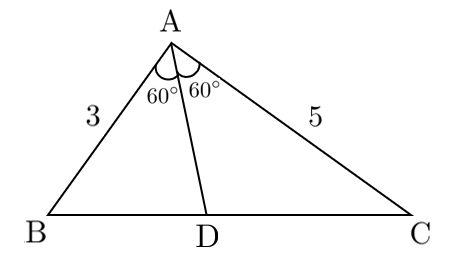
(2) $\textrm{AB}=4$,$\textrm{BC}=6$,$\textrm{AB}=5$ の $\triangle\textrm{ABC}$ において,角の二等分線 $\textrm{AD}$ の長さを求めよ。
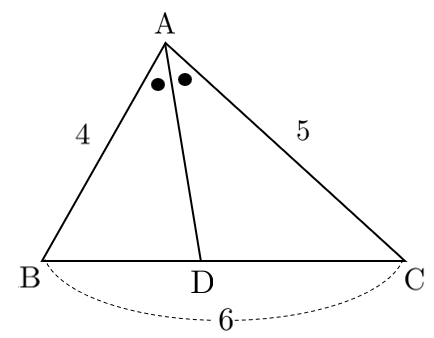
(1) $\textrm{AD}=x$ とおくと
\begin{eqnarray} \triangle\textrm{ABC} &=& \triangle\textrm{ABD}+\triangle\textrm{ACD} \\ \frac{1}{2}\cdot3\cdot5\sin120^\circ &=& \frac{1}{2}\cdot3\cdot x\sin 60^\circ+\frac{1}{2}\cdot5\cdot x\sin60^\circ \\ 3\cdot5 &=& 3\cdot x+5\cdot x \\ x &=& \frac{15}{8} \end{eqnarray}したがって $\displaystyle{\textrm{AD}=\frac{15}{8}}$
(2) $\triangle\textrm{ABC}$ で余弦定理より
$\displaystyle{\cos B=\frac{4^2+6^2-5^2}{2\cdot4\cdot6}=\frac{9}{16}}$
線分 $\textrm{AD}$ は角の二等分線なので
$\textrm{BD}:\textrm{DC}=\textrm{AB}:\textrm{AC}=4:5$
よって $\displaystyle{\textrm{BD}=\frac{4}{9}\textrm{BC}=\frac{8}{3}}$

$\triangle\textrm{ABD}$ で余弦定理より
$\displaystyle{\textrm{AD}^2=4^2+\left(\frac{8}{3}\right)^2-2\cdot4\cdot\frac{8}{3}\cos B=\frac{100}{9}}$
$\textrm{AD}>0$ より $\displaystyle{\textrm{AD}=\frac{10}{3}}$
角の二等分線の長さ(角度が与えられている場合)
(1) $\textrm{AB}=3$,$\textrm{AC}=5$,$\angle\textrm{A}=120^\circ$ の $\triangle\textrm{ABC}$ において,角の二等分線 $\textrm{AD}$ の長さを求めよ。

<三角形の面積を利用して解く>
$\triangle\textrm{ABC} = \triangle\textrm{ABD}+\triangle\textrm{ACD}$ を利用することで、角の二等分線の長さ $\textrm{AD}$ の長さが求まる
(1) $\textrm{AD}=x$ とおくと
\begin{eqnarray} \triangle\textrm{ABC} &=& \triangle\textrm{ABD}+\triangle\textrm{ACD} \\ \frac{1}{2}\cdot3\cdot5\sin120^\circ &=& \frac{1}{2}\cdot3\cdot x\sin 60^\circ+\frac{1}{2}\cdot5\cdot x\sin60^\circ \\ 3\cdot5 &=& 3\cdot x+5\cdot x \\ x &=& \frac{15}{8} \end{eqnarray}したがって $\displaystyle{\textrm{AD}=\frac{15}{8}}$

角の二等分線の長さ(角度が与えられていない場合)
(2) $\textrm{AB}=4$,$\textrm{BC}=6$,$\textrm{AB}=5$ の $\triangle\textrm{ABC}$ において,角の二等分線 $\textrm{AD}$ の長さを求めよ。

- $\triangle\textrm{ABC}$ で余弦定理を用いて、$\cos B$ を求める。
- 『角の二等分線の性質』を利用して $\textrm{BD}$ の長さを求める。
- $\triangle\textrm{ABD}$ で余弦定理を用いて、角の二等分線 $\textrm{AD}$ の長さを求める。
(2) $\triangle\textrm{ABC}$ で余弦定理より
$\displaystyle{\cos B=\frac{4^2+6^2-5^2}{2\cdot4\cdot6}=\frac{9}{16}}$
線分 $\textrm{AD}$ は角の二等分線なので(角の二等分線の性質)
$\textrm{BD}:\textrm{DC}=\textrm{AB}:\textrm{AC}=4:5$
よって $\displaystyle{\textrm{BD}=\frac{4}{9}\textrm{BC}=\frac{8}{3}}$

$\triangle\textrm{ABD}$ で余弦定理より
$\displaystyle{\textrm{AD}^2=4^2+\left(\frac{8}{3}\right)^2-2\cdot4\cdot\frac{8}{3}\cos B=\frac{100}{9}}$
$\textrm{AD}>0$ より $\displaystyle{\textrm{AD}=\frac{10}{3}}$




コメント