数学Ⅰの三角比が最初からよくわからない人必見!
30°,45°,60°における三角比を丁寧に解説しました!
三角比の最初は直角三角形の辺の比を考えることが重要!
ここがわからなければ,三角比はわからないままです!
この投稿を見れば,三角比の基本はばっちり!
三角比の定義
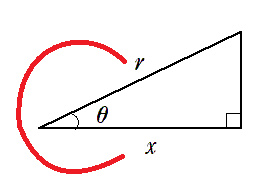
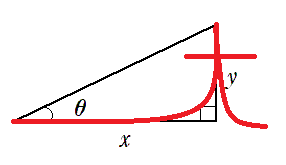
直角三角形の鋭角($90^\circ$ 未満の角)の1つを $\theta$ とし,斜辺の長さを $r$ ,その他の辺の長さを下図のように $x$,$y$ とするとき,三角比の定義は以下のようになる。
※ $x$ のことを $\theta$ の隣の辺なので「隣辺」,$y$ のことを $\theta$ の向かいの辺なので「対辺」とよぶこともある。
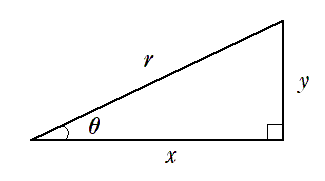
$\displaystyle{\sin\theta=\frac{y}{r}}$, $\displaystyle{\cos\theta=\frac{x}{r}}$, $\displaystyle{\tan\theta=\frac{y}{x}}$
● $\sin\theta$ の覚え方
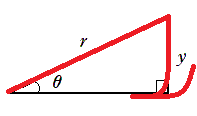
$s$ の筆記体で $\displaystyle{\sin\theta=\frac{y}{r}}$
● $\cos\theta$ の覚え方
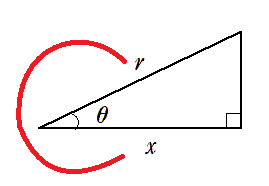
$c$ と書いて $\displaystyle{\cos\theta=\frac{x}{r}}$
● $\tan\theta$ の覚え方
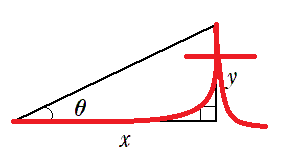
$t$ の筆記体で $\displaystyle{\tan\theta=\frac{y}{x}}$
30°,45°,60° の三角比

30°,45°,60° の三角比は登場機会が多いので,きちんと確認しておこう!
30°,60° の三角比
1辺の長さが 2 の正三角形を半分にすると,
30°,60° の直角三角形ができる
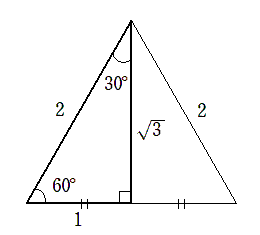
30°,60° の直角三角形の辺の比は $1:2:\sqrt{3}$ である
この直角三角形を用いると,30°,60° の三角比を求めることができる
● 30°の三角比
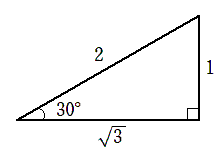
$\displaystyle{\sin30^\circ=\frac{1}{2}}$
$ \displaystyle{\cos30^\circ=\frac{\sqrt{3}}{2}}$
$ \displaystyle{\tan30^\circ=\frac{1}{\sqrt{3}}}$
● 60°の三角比
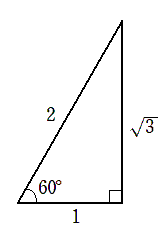
$\displaystyle{\sin60^\circ=\frac{\sqrt{3}}{2}}$
$\displaystyle{ \cos60^\circ=\frac{1}{2}}$
$ \displaystyle{\tan60^\circ=\sqrt{3}}$

30° と 60° の三角比は,同じ $1:2:\sqrt{3}$ の直角三角形から作れるから,似たような値になるよ!
45° の三角比
直角二等辺三角形を用いると,45° の三角比が求まる
直角二等辺三角形の辺の比は $1:1:\sqrt{2}$ である
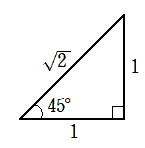
$ \displaystyle{\sin45^\circ=\frac{1}{\sqrt{2}}}$
$ \displaystyle{\cos45^\circ=\frac{1}{\sqrt{2}}}$
$ \displaystyle{\tan45^\circ=1}$
その他の鋭角の三角比

30°,45°,60° 以外の鋭角の三角比はどうなるのかな?
例えば,20$^\circ$ の三角比を考えてみよう
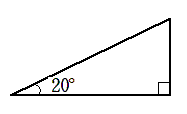
30$^\circ$,45$^\circ$,60$^\circ$ の直角三角形のように,
辺の比を計算で求めることは容易ではない
ちなみに,20$^\circ$ の三角比の値は
$\sin20^\circ=0.3420…$
$\cos20^\circ=0.9397…$
$\tan20^\circ=0.3640…$
角度がどうであれ,実際に長さを測れば三角比の値を求めることができる

教科書に三角比の値の表が載っているよ!
確認してみよう!
鋭角の三角比の値の規則性
30°,45°,60° の三角比の値を表にしてみる
規則性が分かりやすいように $\displaystyle{\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}}$ と書き換える(分母の有理化)
| $\theta$ | 30$^\circ$ | 45$^\circ$ | 60$^\circ$ |
| $\sin\theta$ | $\frac{1}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{3}}{2}$ |
| $\cos\theta$ | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{1}{2}$ |
| $\tan\theta$ | $\frac{1}{\sqrt{3}}$ | $1$ | $\sqrt{3}$ |
$\theta$ が大きくなるにつれて
- $\sin\theta$ は大きくなる
- $\cos\theta$ は小さくなる
- $\tan\theta$ は大きくなる
という規則性があることが分かる
図形から見た規則性

直角三角形を使って三角比の値の規則性を見てみよう!
$\sin\theta$ と $\cos\theta$
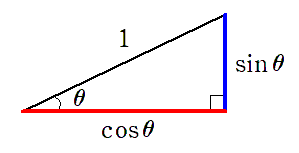
直角三角形の斜辺の長さを $1$
すなわち $r=1$ で固定して三角比の定義を考えると
$$\sin\theta=\frac{y}{r},\cos\theta=\frac{x}{r}$$
$$ \Downarrow r=1とする$$
$$\sin\theta=y,\cos\theta=x$$
$\sin\theta$ は $y$ の長さ,$\cos\theta$ は $x$ の長さになる
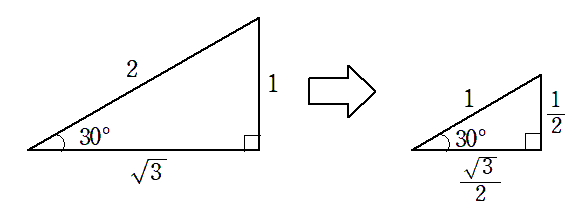
30$^\circ$,60$^\circ$ の直角三角形の斜辺の長さを $1$ にすると
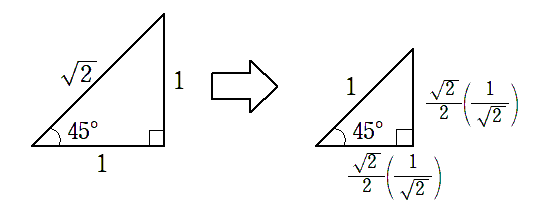
45$^\circ$ の直角三角形の斜辺の長さを $1$ にすると
斜辺の長さが $1$ の 30$^\circ$,45$^\circ$,60$^\circ$ の直角三角形を並べてみると
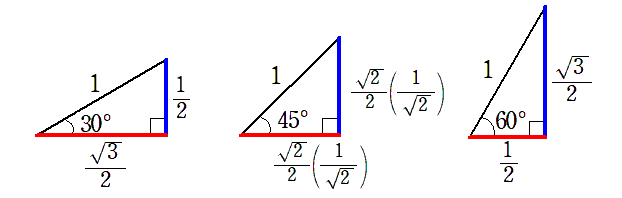
$\theta$ の値が大きくなるにつれて
- 直角三角形の高さは大きくなるので,$\sin\theta$ は大きくなる
- 直角三角形の底辺は小さくなるので,$\cos\theta$ は小さくなる
$\tan\theta$

$\tan\theta$ は直角三角形の何を表しているんだろう?
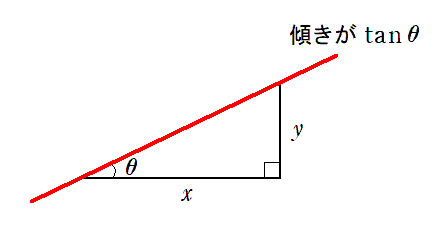
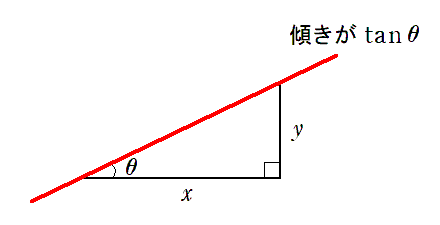
$\tan\theta$ は $\displaystyle\frac{y}{x}$ なので,
直角三角形の斜辺の傾きを表している
30$^\circ$,45$^\circ$,60$^\circ$ の直角三角形を並べてみると
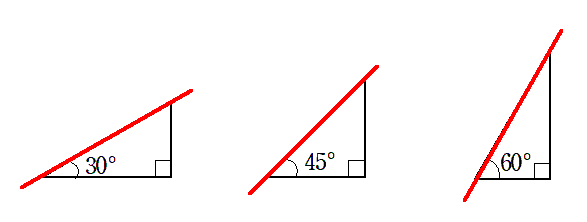
$\theta$ の値が大きくなるにつれて
直角三角形の斜辺の傾きが大きくなるので,$\tan\theta$ は大きくなる
まとめ
● 鋭角の三角比の定義
$\sin\theta=\frac{y}{r},\cos\theta=\frac{x}{r},\tan\theta=\frac{y}{x}$
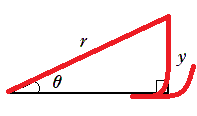
● 30°,45°,60° の三角比の値
| $\theta$ | 30$^\circ$ | 45$^\circ$ | 60$^\circ$ |
| $\sin\theta$ | $\frac{1}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{3}}{2}$ |
| $\cos\theta$ | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{1}{2}$ |
| $\tan\theta$ | $\frac{1}{\sqrt{3}}$ | $1$ | $\sqrt{3}$ |
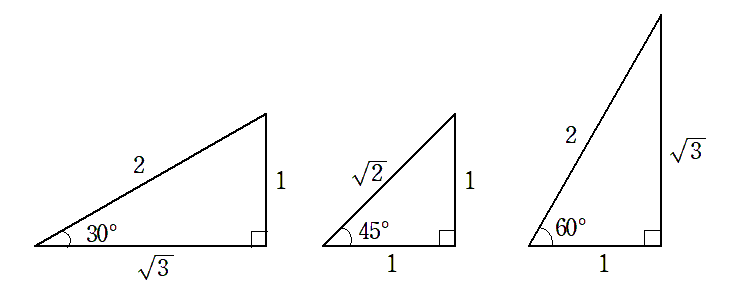
● 鋭角の三角比の値の規則性
$$\sin\theta=\frac{y}{r},\cos\theta=\frac{x}{r}$$
$$ \Downarrow r=1とする$$
$$\sin\theta=y,\cos\theta=x$$

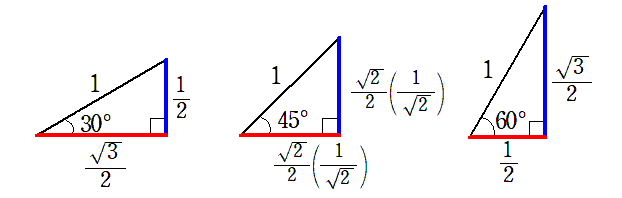
$\theta$ の値が大きくなるにつれて
- 直角三角形の高さは大きくなるので,$\sin\theta$ は大きくなる
- 直角三角形の底辺は小さくなるので,$\cos\theta$ は小さくなる
$\tan\theta$ は $\frac{y}{x}$ なので,
直角三角形の斜辺の傾きを表している

$\theta$ の値が大きくなるにつれて
直角三角形の斜辺の傾きが大きくなるので,$\tan\theta$ は大きくなる

三角比の基本をきちんと理解しておこう!




コメント