直角三角形の1辺と鋭角が分かっている場合,他の辺の長さが求まることを知っていますか?
高校生が意外と知らない「角比を用いて直角三角形の辺の長さを求める方法」をわかりやすく解説しました!
覚えておくのは三角比の定義だけで十分です!

まずは三角比の定義の復習をしよう!
詳しく学びたい人は↓

三角比の定義
直角三角形の鋭角(90$^\circ$ 未満の角)の1つを $\theta$ とし,斜辺の長さを $r$ ,その他の辺の長さを下図のように $x$,$y$ とするとき,三角比の定義は以下のようになる。
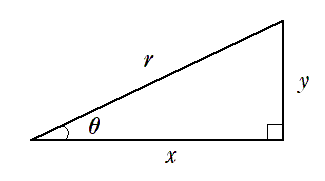
$\displaystyle{\sin\theta=\frac{y}{r}}$, $\displaystyle{\cos\theta=\frac{x}{r}}$, $\displaystyle{\tan\theta=\frac{y}{x}}$
● $\sin\theta$ の覚え方
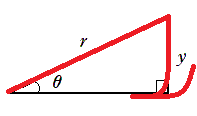
$s$ の筆記体で $\displaystyle{\sin\theta=\frac{y}{r}}$
● $\cos\theta$ の覚え方
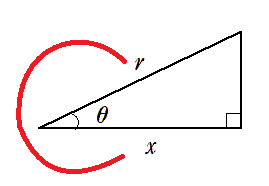
$c$ と書いて $ \displaystyle{ \cos\theta=\frac{x}{r}}$
● $\tan\theta$ の覚え方
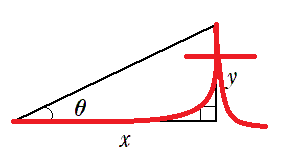
$t$ の筆記体で $ \displaystyle{ \tan\theta=\frac{y}{x}}$
三角比の応用
$ \displaystyle{ \sin\theta=\frac{y}{r}}$ を式変形すると
$y=r\sin\theta$
となる
直角三角形の斜辺の長さ $r$ と $\sin\theta$ があれば高さを求めることができる
同様に
$ \displaystyle{ \cos\theta=\frac{x}{r}}$,$ \displaystyle{ \tan\theta=\frac{y}{x}}$ を式変形すると
$x=r\cos\theta$,$y=x\tan\theta$
となる
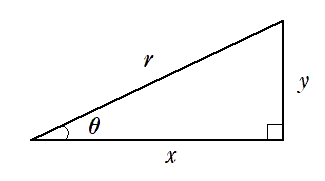
$y=r\sin\theta$,$x=r\cos\theta$,$y=x\tan\theta$

この式は覚えておいた方がいいの?

この式を覚えるよりも三角比の定義を覚えておいて,
式変形して使える方がいいよ!
$\displaystyle{\sin\theta=\frac{y}{r}}$ を覚えておけば,
式変形して $y=r\sin\theta$ が求まるからね!
まとめ
三角比の定義
$\displaystyle{\sin\theta=\frac{y}{r}}$,$\displaystyle{\cos\theta=\frac{x}{r}}$,$ \displaystyle{\tan\theta=\frac{y}{x}}$ を式変形すると
$y=r\sin\theta$,$x=r\cos\theta$,$y=x\tan\theta$
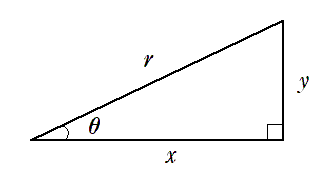
直角三角形の1つの鋭角の三角比の値と1辺の長さが分かっている場合,
他の辺の長さを求めることができる
問題
$C=90^\circ$ である $△ABC$ において次の値を求めよ。
$\sin35^\circ=0.5736$,$\cos35^\circ=0.8192$,$\tan35^\circ=0.7002$ を用いてもよい。
(1) $AB=10$,$A=35^\circ$ のとき,$BC$
(2) $AC=10$,$A=35^\circ$ のとき,$BC$
(3) $AB=6$,$\displaystyle{\cos∠BAC=\frac{1}{3}}$ のとき,$AC$
(4) $BC=5$,$\displaystyle{\sin∠BAC=\frac{3}{5}}$ のとき,$AB$
解答
(1) $AB=10$,$A=35^\circ$ のとき,$BC$
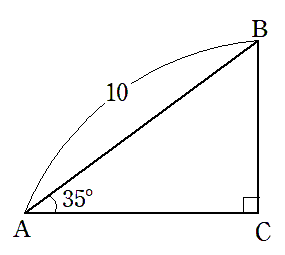
$\displaystyle{\sin35^\circ=\frac{BC}{AB}}$ より
\begin{eqnarray} BC &=& AB\sin35^{\circ} \\\\ &=& 10\times0.5736 \\\\ &=& 5.736 \end{eqnarray}
(2) $AC=10$,$A=35^\circ$ のとき,$BC$
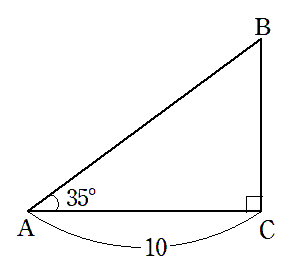
$\displaystyle{\tan35^\circ=\frac{BC}{AC}}$ より
\begin{eqnarray} BC &=& AC\tan35^{\circ} \\\\ &=& 10\times0.7002 \\\\ &=& 7.002 \end{eqnarray}
(3) $AB=6$,$\cos∠BAC=\frac{1}{3}$ のとき,$AC$
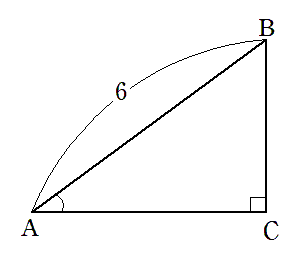
$ \displaystyle{\cos∠BAC=\frac{AC}{AB}}$ より
\begin{eqnarray} AC &=& AB\cos\angle BAC \\\\ &=& 10\times\frac{1}{3} \\\\ &=& 2 \end{eqnarray}
(4) $BC=5$,$\sin∠BAC=\frac{3}{5}$ のとき,$AB$
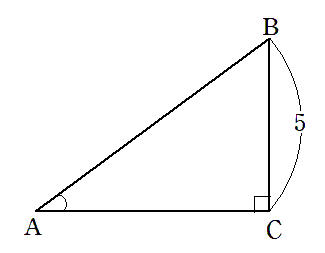
$ \displaystyle{\sin∠BAC=\frac{BC}{AB}}$ より
\begin{eqnarray} AB &=& \frac{BC}{\sin\angle BAC} \\\\ &=& \frac{5}{\frac{3}{5}} \\\\ &=& \frac{25}{3} \end{eqnarray}
三角比を使って直角三角形の辺の長さを求められるようにしよう!




コメント