180°-θの三角比の公式覚えていますか?
忘れがちな三角比の公式の一つです!
式が複雑そうに見えるのが覚えにくい理由として挙げられます!
式だけ見るのではなく,式の意味を理解することが大切です!
この投稿を見れば,180°-θの公式をもう忘れません!
三角比の定義

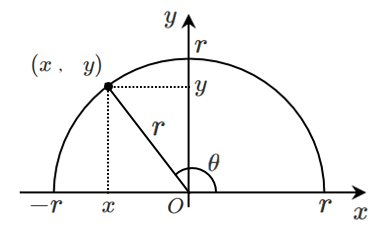
鈍角まで拡張した三角比の定義を復習しよう!
$$\sin\theta=\frac{y}{r},\cos\theta=\frac{x}{r},\tan\theta=\frac{y}{x}$$
詳しい「三角比の拡張」はこれ↓

180°-θ の三角比
$\theta$ に対して $ 180^\circ-\theta$ は図のようになる
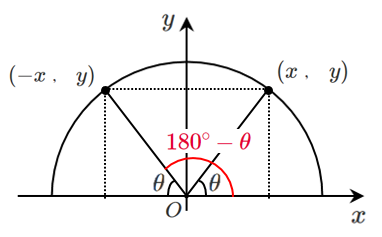
$\theta$ の点 $(x,y)$ に対して
$ 180^\circ-\theta$ の点 $(-x,y)$ は
$y$ 軸に関して対称な点になる
$ 180^\circ-\theta$ の三角比は
$$\sin(180^\circ-\theta)=\frac{y}{r}$$
$$\cos(180^\circ-\theta)=\frac{-x}{r}=-\frac{x}{r}$$
$$\tan(180^\circ-\theta)=\frac{y}{-x}=-\frac{y}{x}$$
ここで
$$\sin\theta=\frac{y}{r},\cos\theta=\frac{x}{r},\tan\theta=\frac{y}{x}$$
なので
$$\sin(180^\circ-\theta)=\sin\theta$$
$$\cos(180^\circ-\theta)=-\cos\theta$$
$$\tan(180^\circ-\theta)=-\tan\theta$$

この式は見たことあるんだけど,すぐ忘れちゃうんだよね…

この式で覚えない方がいいよ!
180°-θ の覚え方
$●+■=180^\circ$ とすると
$\sin●=\sin■$(足して $ 180^\circ$ の $\sin$ は同じ)
$\cos●=-\cos■$(足して $ 180^\circ$ の $\cos$ は異符号)
$\tan●=-\tan■$(足して $ 90^\circ$ の $\tan$ は異符号)

こんな感じで覚えよう!
180°-θ の具体例
● 三角比の表
| $\theta$ | $ 0^\circ$ | $ 30^\circ$ | $ 45^\circ$ | $ 60^\circ$ | $ 90^\circ$ | $ 120^\circ$ | $ 135^\circ$ | $ 150^\circ$ | $ 180^\circ$ |
| $\sin\theta$ | $0$ | $\frac{1}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{3}}{2}$ | $1$ | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{1}{2}$ | $0$ |
| $\cos\theta$ | $1$ | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{1}{2}$ | $0$ | $-\frac{1}{2}$ | $-\frac{\sqrt{2}}{2}$ | $-\frac{\sqrt{3}}{2}$ | $-1$ |
| $\tan\theta$ | $0$ | $\frac{1}{\sqrt{3}}$ | $1$ | $\sqrt{3}$ | × | $-\sqrt{3}$ | $-1$ | $-\frac{1}{\sqrt{3}}$ | $0$ |
$$\sin30^\circ=\sin150^\circ$$
$$\sin45^\circ=\sin135^\circ$$
$$\sin60^\circ=\sin120^\circ$$
足して $ 180^\circ$ の $\sin$ は同じ
$$\cos30^\circ=-\cos150^\circ$$
$$\cos45^\circ=-\cos135^\circ$$
$$\cos60^\circ=-\cos120^\circ$$
足して $ 180^\circ$ の $\cos$ は異符号
(マイナスをつけたら等しい)
$$\tan30^\circ=-\tan150^\circ$$
$$\tan45^\circ=-\tan135^\circ$$
$$\tan60^\circ=-\tan120^\circ$$
足して $ 90^\circ$ の $\tan$ は異符号
(マイナスをつけたら等しい)
まとめ
● $ 180^\circ-\theta$ の三角比
$\sin(180^\circ-\theta)=\sin\theta$
$\cos(180^\circ-\theta)=-\cos\theta$
$\tan(180^\circ-\theta)=-\tan\theta$
● $ 180^\circ-\theta$ の三角比の覚え方
$●+■=180^\circ$ とすると
$\sin●=\sin■$(足して $ 180^\circ$ の $\sin$ は同じ)
$\cos●=-\cos■$(足して $ 180^\circ$ の $\cos$ は異符号)
$\tan●=-\tan■$(足して $ 90^\circ$ の $\tan$ は異符号)
● $ 180^\circ-\theta$ の三角比を用いると $ 90^\circ$ 以下の三角比で表すことができる
例 $\sin150^\circ=\sin30^\circ$
$\cos120^\circ=-\cos60^\circ$
$\tan135^\circ=-\tan45^\circ$
問題
次の三角比を $ 90^\circ$ 以下の三角比で表せ。
(1) $\sin160^\circ$
(2) $\cos130^\circ$
(3) $\tan110^\circ$
解答
(1) $\sin160^\circ=\sin20^\circ$
足して $ 180^\circ$ の $\sin$ は同じ
(2) $\cos130^\circ=-\cos50^\circ$
足して $ 180^\circ$ の $\cos$ は異符号
(3) $\tan110^\circ=-\tan70^\circ$
足して $ 180^\circ$ の $\tan$ は異符号




コメント