相関
2つのデータの間に
一方が増えると他方も増える
一方が増えると他方が減る
という傾向がみられるとき
この2つのデータは「相関がある」という
例えば,身長と体重は,
一方が増えると他方も増える傾向にあるので
「相関がある」という
正の相関と負の相関

相関には「正の相関」と「負の相関」の2種類あるよ!
正の相関
一方が増えると他方も増える傾向
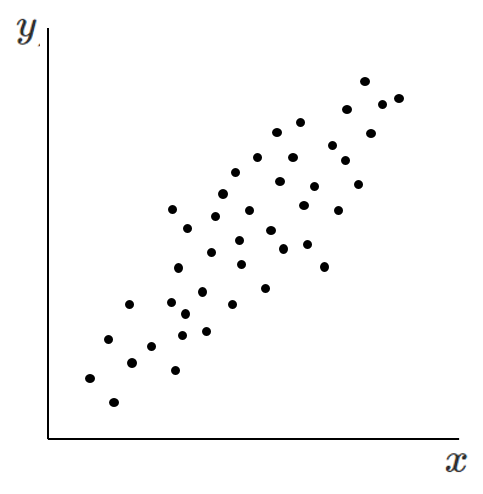
負の相関
一方が増えると他方が減る傾向
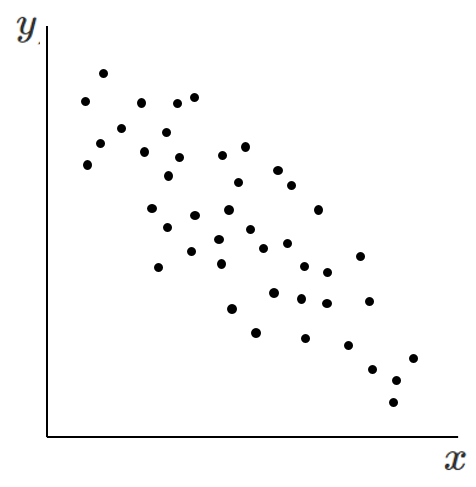
相関がない
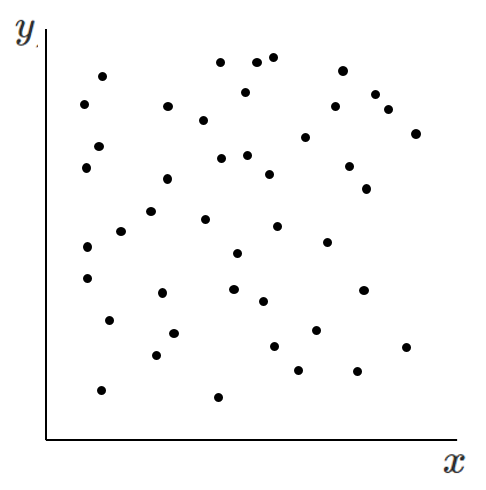
相関係数

「相関係数」を学ぶ前に「標準偏差」と「共分散」から!
分散
$(分散)=(偏差の2乗の平均)$

分散を求めたら標準偏差が求まるよ!
次のデータの分散を求めよ
$x 1 3 5 7 9$
| $x_1$ | $x_2$ | $x_3$ | $x_4$ | $x_5$ | 合計 | 平均 | |
| $x$ | $1$ | $3$ | $5$ | $7$ | $9$ | $25$ | $\bar{x}=5$ |
| 偏差 $x-\bar{x}$ | $-4$ | $-2$ | $0$ | $2$ | $4$ | $0$ | / |
| 偏差の2乗 $(x-\bar{x})^2$ | $16$ | $4$ | $0$ | $4$ | $16$ | $40$ | $s^2=8$ |
偏差の2乗の和が $40$
(分散)=(偏差の2乗の平均) なので
分散 $\displaystyle s^2=\frac{1}{5}・40=8$
詳しくはこれ↓

共分散
$x$ と $y$ の共分散 $s_{xy}$ は
$\displaystyle s_{xy}=\frac{1}{n}\{(x_1-\overline{x})(y_1-\overline{y})+(x_2-\overline{x})(y_2-\overline{y})+……+(x_n-\overline{x})(y_n-\overline{y})\}$
共分散の符号と相関関係
散布図を以下のように $x$ の平均値 $\overline{x}$ と $y$ の平均値 $\overline{y}$ で4つの領域に分ける
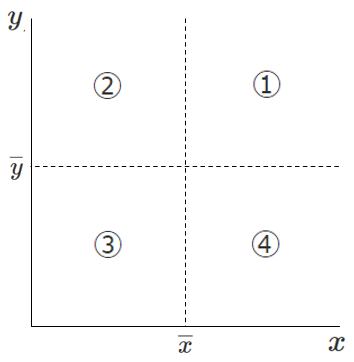
4つの領域について,偏差の符号をみると
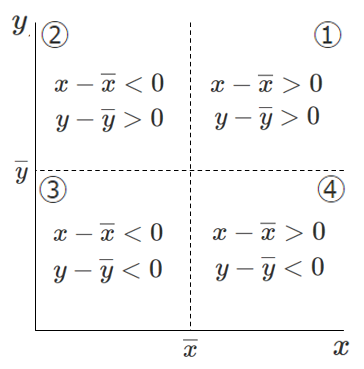
$(xとyの共分散)=(xの偏差とyの偏差の積の平均)$ なので
相関係数の計算式
分子が $x$ と $y$ の共分散なので
相関係数が正のときは正の相関,負のときは負の相関がある
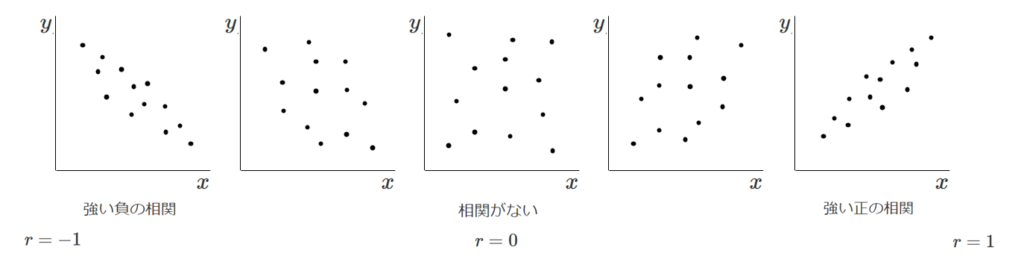
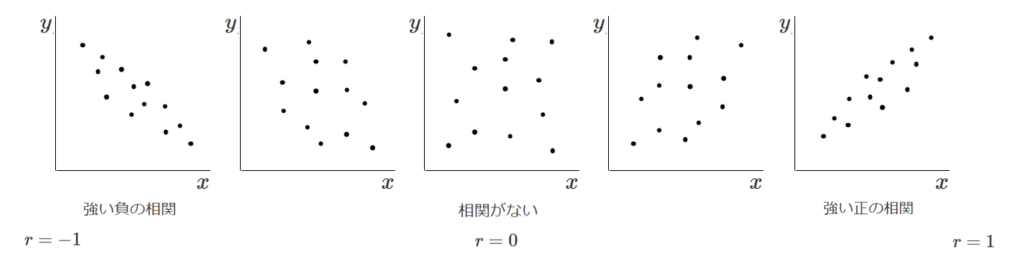
相関係数 $r$ は $-1≦r≦1$ で
問題
次のデータの相関係数を求めよ
\begin{array}{c|ccccc} x & 1 & 3 & 5 & 7 & 9 \\ \hline y & 1 & 5 & 7 & 3 & 9 \\ \end{array}
| $x_1$ | $x_2$ | $x_3$ | $x_4$ | $x_5$ | 合計 | 平均 | |
| $x$ | $1$ | $3$ | $5$ | $7$ | $9$ | $25$ | $\overline{x}=5$ |
| $y$ | $1$ | $5$ | $7$ | $3$ | $9$ | $25$ | $\overline{x}=5$ |
| $x-\overline{x}$ | $-4$ | $-2$ | $0$ | $2$ | $4$ | $0$ | / |
| $y-\overline{y}$ | $-4$ | $0$ | $2$ | $-2$ | $4$ | $0$ | / |
| $(x-\overline{x})^2$ | $16$ | $4$ | $0$ | $4$ | $16$ | $40$ | $s_x^2=8$ |
| $(y-\overline{y})^2$ | $16$ | $0$ | $4$ | $4$ | $16$ | $40$ | $s_y^2=8$ |
| $(x-\overline{x})(y-\overline{y})$ | $16$ | $0$ | $0$ | $-4$ | $16$ | $28$ | $\displaystyle s_{xy}=\frac{28}{5}$ |
$x$ の分散 $s_x^2=8$,$y$ の分散 $s_y^2=8$,$x$ と $y$ の共分散 $\displaystyle s_{xy}=\frac{28}{5}$ より
$\displaystyle(xとyの相関係数)=\frac{(xとyの共分散)}{\sqrt{(xの分散)}×\sqrt{(yの分散)}}$ を用いて
相関係数 $\displaystyle r=\frac{\frac{28}{5}}{\sqrt{8}×\sqrt{8}}=0.7$
$x$ と $y$ には正の相関がある
まとめ
● 相関係数の求め方
$\displaystyle(xとyの相関係数)=\frac{(xとyの共分散)}{\sqrt{(xの分散)}×\sqrt{(yの分散)}}$
ここで $(分散)=(偏差の2乗の平均)$
$(xとyの共分散)=(xの偏差とyの偏差の積の平均)$
● 相関係数の特徴
相関係数 $r$ は $-1≦r≦1$ で
・ $1$ に近づくほど強い正の相関がある
・ $-1$ に近づくほど強い負の相関がある
・ $0$ に近いと相関がない

「相関係数」も表にして求めた方がいいね!




コメント