空間のベクトルの成分表示

平面のベクトルと同様に,空間のベクトルも成分表示を考えよう!
平面のベクトルの成分表示はこれ↓

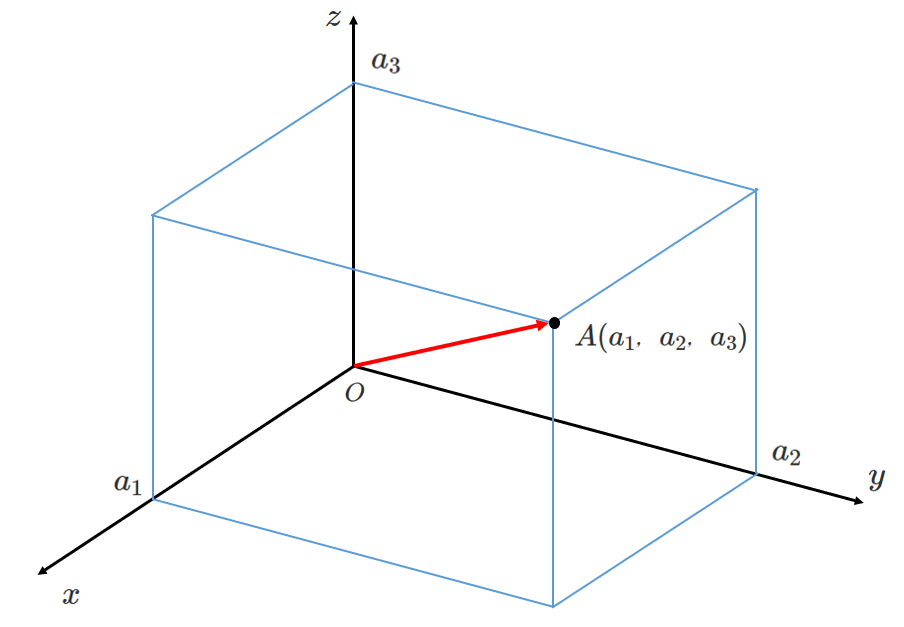
$A(a_1,a_2,a_3)$ であるとき,
$\overrightarrow{OA}=(a_1,a_2,a_3)$
と表す
$a_1$ を $x$ 成分,$a_2$ を $y$ 成分,$a_3$ を $z$ 成分 という

平面のベクトルに $z$ 成分が加わるだけだね!
成分表示におけるベクトルの大きさ
$\vec{a}=(1,3,2)$ の大きさ $|\vec{a}|$ を考える
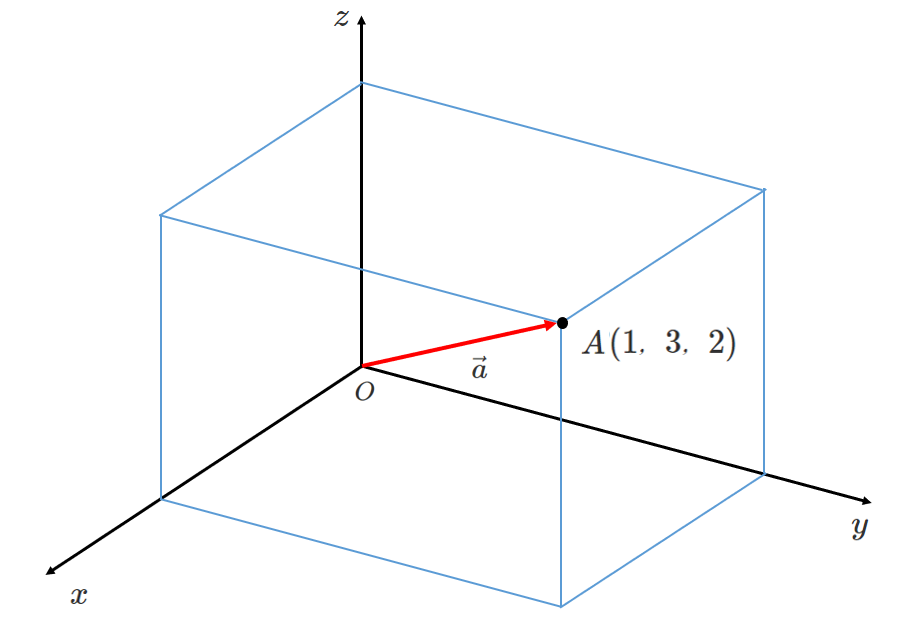
$|\vec{a}|$ は $OA$ の長さと等しいので
\begin{eqnarray} |\vec{a}| &=& OA \\\\ &=& \sqrt{1^2+3^2+2^2} \\\\ &=& \sqrt{14} \end{eqnarray}
以上より,成分表示におけるベクトルの大きさは以下のようになる
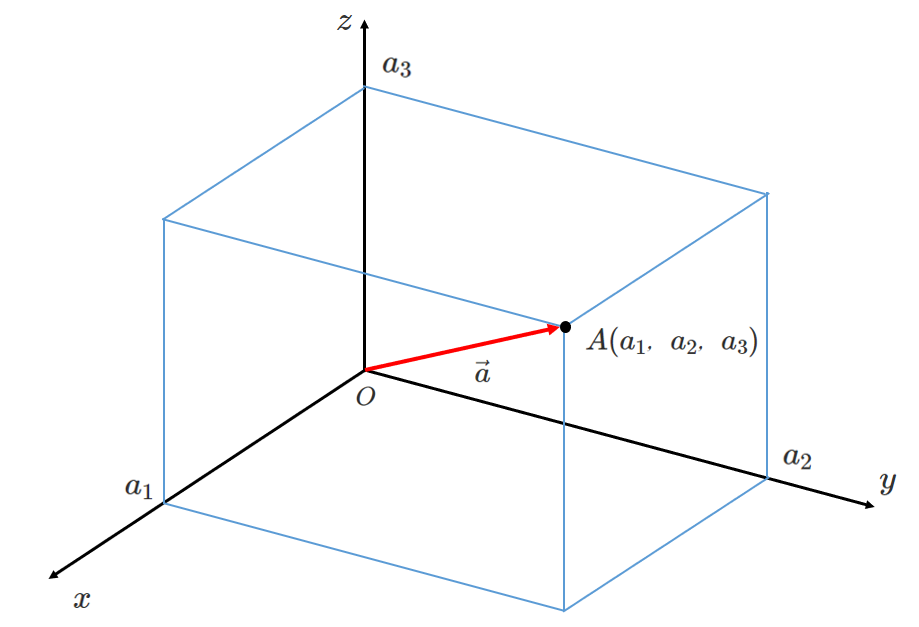

$2$ 点間の距離は「$2$ 乗の和のルート」!
成分表示の計算

成分表示の計算も,平面のベクトルに $z$ 成分が加わるだけと考えよう!
1 $(a_1,a_2,a_3)+(b_1,b_2,b_3)=(a_1+b_1,a_2+b_2,a_3+b_3)$
2 $(a_1,a_2,a_3)-(b_1,b_2,b_3)=(a_1-b_1,a_2-b_2,a_3-b_3)$
3 $k(a_1,a_2,a_3)=(ka_1,ka_2,ka_3)$
原点以外が始点のベクトル
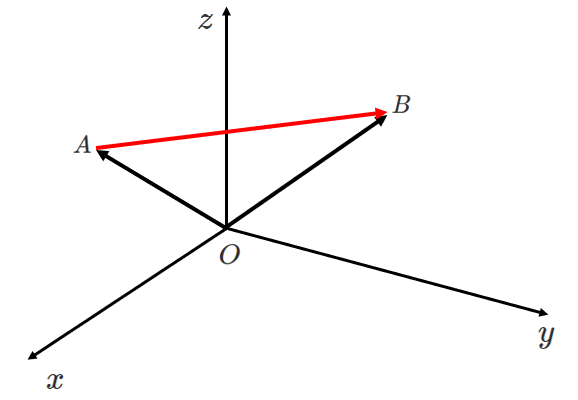
座標平面上にある2点 $A(a_1,a_2,a_3)$,$B(b_1,b_2,b_3)$ について
$\overrightarrow{AB}$ を成分で表すと
$\overrightarrow{AB}= \overrightarrow{OB}- \overrightarrow{OA}$ より(ベクトルの減法)
\begin{eqnarray} \overrightarrow{AB} &=& \overrightarrow{OB}- \overrightarrow{OA} \\\\ &=& (b_1,b_2,b_3)-(a_1,a_2,a_3) \\\\ &=& (b_1-a_1,b_2-a_2,b_3-a_3) \end{eqnarray}
空間のベクトルの内積

内積も平面のベクトルと同様!
ベクトルの内積はこれ↓

$\vec{a}$ と $\vec{b}$ のなす角を $\theta$ とすると
$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta$
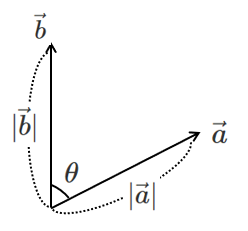
なす角 $\theta$ は「始点を合わせたときの角度」のこと
また,$0^\circ≦\theta≦180^\circ$
なす角 $\theta$ を求めたい場合は
$\displaystyle{\cos\theta=\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}}$
を用いる
空間のベクトルの成分表示における内積
$\vec{a}=(a_1,a_2,a_3)$,$\vec{b}=(b_1,b_2,b_3)$ のとき
$\vec{a}\cdot\vec{b}=a_1b_1+a_2b_2+a_3b_3$
<証明>
$\vec{a}=(a_1,a_2,a_3)$,$\vec{b}=(b_1,b_2,b_3)$ とする
$|\vec{a}-\vec{b}|^2=|\vec{a}|^2-2\vec{a}\cdot\vec{b}+|\vec{b}|^2$
$\vec{a}-\vec{b}=(a_1-b_1,a_2-b_2,a_3-b_3)$ より
$(a_1-b_1)^2+(a_2-b_2)^2+(a_3-b_3)^2$
$=({a_1}^2+{a_2}^2+{a_3}^2)-2\vec{a}\cdot\vec{b}+({b_1}^2+{b_2}^2+{b_3}^2)$
整理すると
$\vec{a}\cdot\vec{b}=a_1b_1+a_2b_2+a_3b_3$

内積に関する問題を解いてみよう!
次の $2$ つのベクトル $\vec{a}$,$\vec{b}$ のなす角 $\theta$ を求めよ。
$\vec{a}=(2,3,1)$,$\vec{b}=(-3,-1,2)$
\begin{eqnarray} \vec{a}\cdot\vec{b} &=& 2\cdot(-3)+3\cdot(-1)+1\cdot2 \\ &=& -7 \\\\ |\vec{a}| &=& \sqrt{2^2+3^2+1^2} \\ &=& \sqrt{14} \\\\ |\vec{b}| &=& \sqrt{(-3)^2+(-1)^2+2^2} \\ &=& \sqrt{14} \end{eqnarray}
よって
\begin{eqnarray} \cos\theta &=& \frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|} \\\\ &=& \frac{-7}{\sqrt{14}\sqrt{14}} \\\\ &=& -\frac{1}{2} \end{eqnarray}$0^{\circ}≦\theta≦180^{\circ}$ であるから
$\theta=120 ^{\circ} $

平面の復習にもなるね!
まとめ
● 空間のベクトルの成分表示

$A(a_1,a_2,a_3)$ であるとき,
$\overrightarrow{OA}=(a_1,a_2,a_3)$
$\vec{a}=(a_1,a_2,a_3)$ のとき
$|\vec{a}|=\sqrt{{a_1}^2+{a_2}^2+{a_3}^2}$
● 空間のベクトルの成分表示の計算
1 $(a_1,a_2,a_3)+(b_1,b_2,b_3)=(a_1+b_1,a_2+b_2,a_3+b_3)$
2 $(a_1,a_2,a_3)-(b_1,b_2,b_3)=(a_1-b_1,a_2-b_2,a_3-b_3)$
3 $k(a_1,a_2,a_3)=(ka_1,ka_2,ka_3)$
● 空間のベクトルの内積
$\vec{a}$ と $\vec{b}$ のなす角を $\theta$ とすると
$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta$
なす角 $\theta$ を求めたい場合は
$\displaystyle{\theta=\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}}$
● 空間のベクトルの内積の成分表示
$\vec{a}=(a_1,a_2,a_3)$,$\vec{b}=(b_1,b_2,b_3)$ のとき
$\vec{a}\cdot\vec{b}=a_1b_1+a_2b_2+a_3b_3$

平面のベクトルに $z$ 成分が加わるだけと考えよう!




コメント