高校数学Ⅰの図形と計量において、『三角形の内接円の半径』を求める問題は頻出です!
『三角形の内接円の半径』を求める公式を理解しておけば、簡単に解くことができます!
この投稿を見れば、『三角形の内接円の半径』を求める問題を必ず解けるようになります!
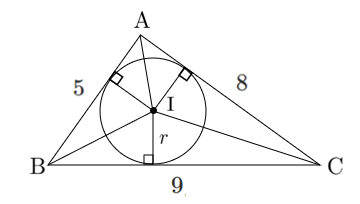
問題
余弦定理より $\displaystyle{\cos A=\frac{8^2+5^2-9^2}{2\cdot8\cdot5}=\frac{1}{10}}$
$\sin^2 A+\cos^2 A=1$ より $\displaystyle{\sin^2 A=1-\cos^2 A=1-\left(\frac{1}{10}\right)^2=\frac{99}{100}}$
$0^\circ<A<180^\circ$ より、$\sin A>0$ なので $\displaystyle{\sin A=\frac{3\sqrt{11}}{10}}$
したがって $\displaystyle{S=\frac{1}{2}\cdot8\cdot5\sin A=6\sqrt{11}}$
$\displaystyle{S=\frac{1}{2}r(a+b+c)}$ より
$\displaystyle{6\sqrt{11}=\frac{1}{2}r(9+8+5)}$
よって $\displaystyle{r=\frac{6\sqrt{11}}{11}}$
三角形の内接円とは
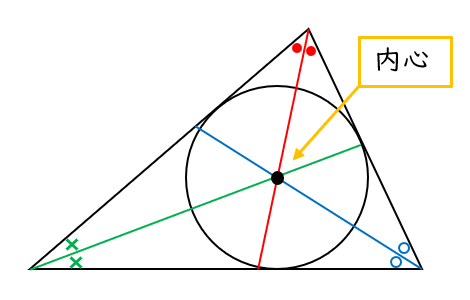
三角形の内接円とは、三角形の内部にあり、すべての辺に接する円のことです。
内接円の中心のことを 内心 といいます。
内心は角の二等分線の交点です。
三角形の内接円の半径に関する公式
$\triangle\textrm{ABC}$ の内接円の半径を $r$,面積を $S$ とすると
$\displaystyle{S=\frac{1}{2}r(a+b+c)}$
3辺の長さと面積から内接円の半径が求まる
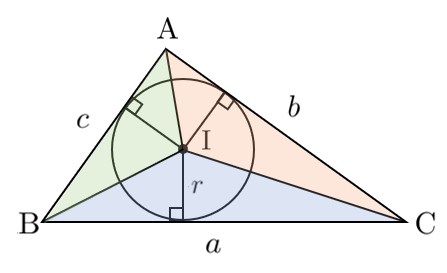
<証明>
$\triangle\textrm{ABC}=\triangle\textrm{IBC}+\triangle\textrm{ICA}+\triangle\textrm{IAB}$ より(内接円の中心を $I$ とする)
$\displaystyle{S=\frac{1}{2}ar+\frac{1}{2}br+\frac{1}{2}cr=\frac{1}{2}r(a+b+c)}$
問題解説
三角形の3辺の長さから三角形の面積を求める
その手順として
① 余弦定理で $\cos A$ の値を求める($\cos B$ でも $\cos C$ でもよい)
② $\sin^2A+\cos^2A=1$ を用いて $\sin A$ を求める
③ 三角形の面積の公式 $\displaystyle{S=\frac{1}{2}bc\sin A}$ を用いて面積を求める
① 余弦定理より $\displaystyle{\cos A=\frac{8^2+5^2-9^2}{2\cdot8\cdot5}=\frac{1}{10}}$
② $\sin^2 A+\cos^2 A=1$ より $\displaystyle{\sin^2 A=1-\cos^2 A=1-\left(\frac{1}{10}\right)^2=\frac{99}{100}}$
$0^\circ<A<180^\circ$ より、$\sin A>0$ なので $\displaystyle{\sin A=\frac{3\sqrt{11}}{10}}$
③ したがって $\displaystyle{S=\frac{1}{2}\cdot8\cdot5\sin A=6\sqrt{11}}$
三角形の面積と3辺の長さを用いて、公式から三角形の内接円の半径を求める
$\displaystyle{S=\frac{1}{2}r(a+b+c)}$ より
$\displaystyle{6\sqrt{11}=\frac{1}{2}r(9+8+5)}$
よって $\displaystyle{r=\frac{6\sqrt{11}}{11}}$





コメント