高校数学Ⅱで習う『円の方程式の基本形と一般形』について解説!
円の方程式には、基本形と一般形という2種類の形があります!
問題によって、基本形と一般形を使い分ける必要があります!
この投稿を見れば、『円の方程式の基本形と一般形』はバッチリ!
円の方程式の基本形
点 $(a,b)$ を中心とする半径 $r$ の円の方程式は
$(x-a)^2+(y-b)^2=r^2$

中心と半径が分かる形が「基本形」と呼ばれている!
円の方程式の基本はこれ↓
円の方程式の一般形
$(x-1)^2+(y-3)^2=4$
$x^2-2x+1+y^2-6y+9=4$
$x^2+y^2-2x-6y+6=0$

円の方程式の基本形を展開すると,
$x^2+y^2+○x+□y+△=0$ という形に変形できる!
これを一般形というよ!

円の方程式は2種類の形があるんだね!
一般形から基本形の式変形

基本形 $(x-a)^2+(y-b)^2=r^2$ から
一般形 $x^2+y^2+lx+my+n=0$ の式変形は展開すればできる!
一般形から基本形の式変形はどうやってするのかな?
$x^2+y^2+2x-4y+4=0$
$x^2+2x$$+$$y^2-4y$$+4=0$
$(x+1)^2-1^2$$+$$(y-2)^2-2^2$$+4=0$
$(x+1)^2-1+(y-2)^2-4+4=0$
$(x+1)^2+(y-2)^2=1$

この式変形を見て何か思い出さない?

$x$ と $y$ でそれぞれ平方完成すればいいね!
基本形を使う問題

中心と半径を使う問題は基本形を使おう!
ただし,円の中心は第1象限にあるものとする。
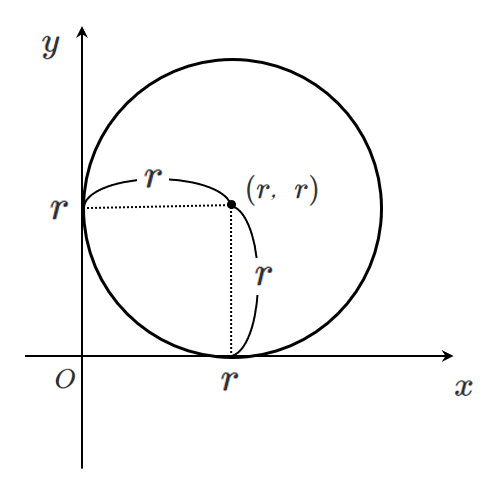
円の中心が第1象限にあり,$x$ 軸と $y$ 軸の両方と接するので
円の半径を $r$ $(r>0)$ とすると,円の中心は $(r,r)$ である
円の方程式は $(x-r)^2+(y-r)^2=r^2$
点 $(2,1)$ を通るので ←通るは代入
$(2-r)^2+(1-r)^2=r^2$
$4-4r+r^2+1-2r+r^2=r^2$
$r^2-6r+5=0$
$(r-1)(r-5)=0$
$r=1,5$
求める円の方程式は
$(x-1)^2+(y-1)^2=1$
$(x-5)^2+(y-5)^2=25$
一般形を使う問題

中心と半径に関する情報がないときは一般形を使おう!
特に,3点が与えられている問題は必ず一般形!
求める円の方程式を $x^2+y^2+lx+my+n=0$ とすると
$(4,2)$ を通るので $4^2+2^2+4l+2m+n=0$
すなわち $4l+2m+n=-20$ $\cdots\cdots$ ①
$(3,1)$ を通るので $3^2+1^2+3l+m+n=0$
すなわち $3l+m+n=-10$ $\cdots\cdots$ ②
$(1,3)$ を通るので $1^2+3^2+l+3m+n=0$
すなわち $l+3m+n=-10$ $\cdots\cdots$ ③
①ー②より $l+m=-10$ $\cdots\cdots$ ④
①ー③より $3l-m=-10$ $\cdots\cdots$ ⑤
④,⑤を解いて $l=-5,m=-5$
これらを①に代入して $n=10$
求める円の方程式は $x^2+y^2-5x-5y+10=0$

それぞれのメリットを理解して使い分けられるようにしよう!
まとめ
● 円の方程式の基本形
$(x-a)^2+(y-b)^2=r^2$
中心と半径が分かる形
● 円の方程式の一般形
$x^2+y^2+lx+my+n=0$
● 一般形から基本形の式変形
$x$ と $y$ についてそれぞれ平方完成する
● 基本形と一般形の使い分け
円の中心と半径に関するヒントがある場合は基本形,ない場合は一般形

基本形と一般形を理解して使いこなすことができたら,円の方程式は完璧!




コメント