高校数学Ⅰの『図形と計量』における応用問題の1つである『四面体の垂線の長さ』を求める問題をわかりやすく解説!
ポイントは、四面体の体積を2通りで表すこと!
問題
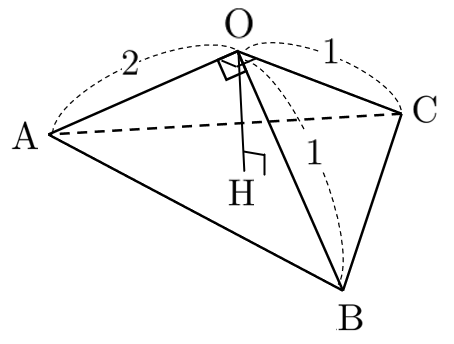
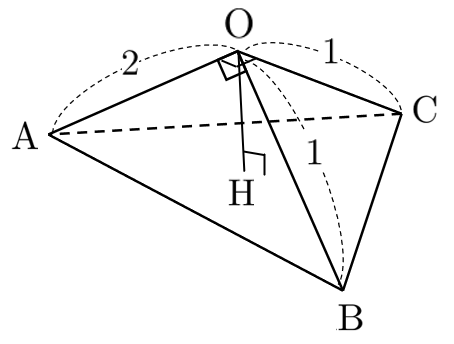
$\angle\textrm{AOB}=\angle\textrm{AOC}=90^\circ$、$\triangle\textrm{ABC}$ の面積が $\displaystyle{\frac{3}{2}}$ である右図の四面体 $\textrm{OABC}$ について、頂点 $\textrm{O}$ から平面 $\textrm{ABC}$ に下ろした垂線の長さ $\textrm{OH}$ を求めよ。
解答
<四面体の体積を2通りで表すことで、垂線の長さを求めることができる>
① 底面を $\triangle\textrm{OBC}$ として、高さが $\textrm{OA}$
② 底面を $\triangle\textrm{ABC}$ として、高さが $\textrm{OH}$
同じ四面体の体積を表しているので、①と②をイコールで結べば垂線 $\textrm{OH}$ が求まる
$\triangle\textrm{OBC}$ を底面としたときの体積 $V$ は
\begin{eqnarray} V &=& \frac{1}{3}\times(底面 \textrm{OBC})\times(高さ \textrm{OA}) \\ &=& \frac{1}{3}\times\left(\frac{1}{2}\cdot 1\cdot 1\right)\times 2 \\ &=& \frac{1}{3} \cdots ① \end{eqnarray}$\triangle\textrm{ABC}$ を底面としたときの体積 $V$ は
\begin{eqnarray} V &=& \frac{1}{3}\times(底面 \textrm{ABC})\times(高さ \textrm{OH}) \\ &=& \frac{1}{3}\times\frac{3}{2}\times \textrm{OH} \\ &=& \frac{1}{2}\textrm{OH} \cdots ① \end{eqnarray}①、②より $\displaystyle{\frac{1}{2}\textrm{OH}=\frac{1}{3}}$
したがって $\displaystyle{\textrm{OH}=\frac{2}{3}}$
あなたのオススメ




コメント