
ベクトルの式から点の位置を求めよう!
今回の問題

次の問題を解けるようになろう!

どこから手をつけたらいいか分からない…

初見で解くのは難しい!
コツをつかめば必ず解けるよ!
ベクトルの差の分解

問題を解くために復習から!
$\overrightarrow{△□}=\overrightarrow{●□}- \overrightarrow{●△}$
例えば
$\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}$
$\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}$
詳しくはこれ↓

内分点におけるベクトル
辺 $AB$ を $m:n$ に内分する点 $P$
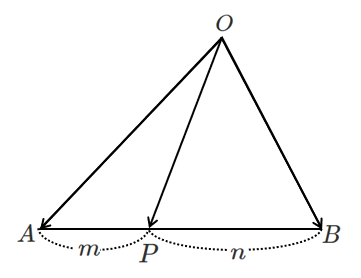
$\displaystyle{\overrightarrow{OP}=\frac{n\overrightarrow{OA}+m\overrightarrow{OB}}{m+n}}$
詳しくはこれ↓

ベクトルの式から点の位置を求める

まずは基本の問題から!
点 $D$ は線分 $BC$ を $3:2$ に内分する点
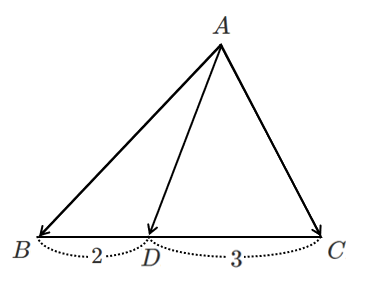

内分点におけるベクトルを表す式から,点の位置が求まるね!

それじゃあ,冒頭の問題にチャレンジしてみよう!
手順1 始点をそろえる

まずは始点を $A$ にそろえよう!
そのときに,「ベクトルの差の分解」を用いよう!
手順2 $P$ の位置を求めたいので $\overrightarrow{AP}$ を求める
\begin{eqnarray} 2\overrightarrow{AP}+3(\overrightarrow{AP}-\overrightarrow{AB})+4(\overrightarrow{AP}-\overrightarrow{AC}) &=& \vec{0} \\\\ 9\overrightarrow{AP} &=& 3\overrightarrow{AB}+4\overrightarrow{AC} \\\\ \overrightarrow{AP} &=& \frac{3\overrightarrow{AB}+4\overrightarrow{AC}}{9} \end{eqnarray}
手順3 内分点におけるベクトルを作る
\begin{eqnarray} \overrightarrow{AP} &=& \frac{3\overrightarrow{AB}+4\overrightarrow{AC}}{9} \\\\ &=& \frac{□}{□}\frac{3\overrightarrow{AB}+4\overrightarrow{AC}}{□} \\\\ \end{eqnarray}
このような分数を作って,□に数字を入れていこう!
まずは,$3\overrightarrow{AB}+4\overrightarrow{AC}$ の下の□には何が入るといいかな?

$7$ が入ると内分点におけるベクトルになりそう!
\begin{eqnarray} \overrightarrow{AP} &=& \frac{3\overrightarrow{AB}+4\overrightarrow{AC}}{9} \\\\ &=& \frac{□}{□}\frac{3\overrightarrow{AB}+4\overrightarrow{AC}}{7} \\\\ \end{eqnarray}

いい感じ!
残りの□には何が入るかな?

$\displaystyle{\frac{7}{9}}$ にしたら元の式と一致しそう!

これで式変形は完了!
あとは $P$ の位置を考えてみよう!
$\displaystyle{\overrightarrow{AD}=\frac{3\overrightarrow{AB}+4\overrightarrow{AC}}{7}}$ とすると
$\displaystyle{\overrightarrow{AD}=\frac{3\overrightarrow{AB}+4\overrightarrow{AC}}{4+3}}$ より
点 $D$ は辺 $BC$ を $4:3$ に内分する点
$\displaystyle{\overrightarrow{AP}=\frac{7}{9}\overrightarrow{AD}}$ より,
点 $P$ は線分 $AD$ を $7:2$ に内分する点
図にしてみると
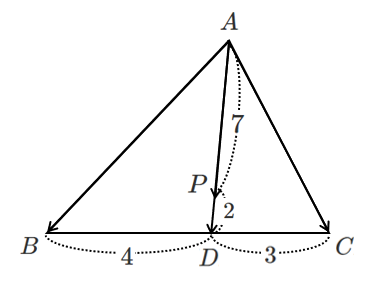
線分 $BC$ を $4:3$ に内分する点を $D$ とすると,点 $P$ は線分 $AD$ を $7:2$ に内分する点

式変形がポイント!
あとは内分点におけるベクトルが理解できていれば解ける!




コメント