2021年 共通テストⅡB 第１問 [1] 三角関数（本試）

第１問「三角関数」の問題

第１問「三角関数」の分析と対策

問題で扱われている分野と力

• 三角関数の値　$\boxed{\mathbf{ア}}$，$\boxed{\mathbf{オ}}，\boxed{\mathbf{カ}}$
• 三角関数の合成　$\boxed{\mathbf{イ}}$
• 三角関数の最大　$\boxed{\mathbf{ウ}}，\boxed{\mathbf{エ}}$，$\boxed{\mathbf{コ}}～\boxed{\mathbf{ス}}$
• 加法定理と合成　$\boxed{\mathbf{キ}}，\boxed{\mathbf{ケ}}$

問題の分析

(1) は

• 三角関数の値
• 三角関数の合成
• 三角関数の最大値

と基本的なレベルの問題となっている

(2) は三角関数の合成を

機械的に解いている受験生にとっては難しい問題

だった

普段は $\sin$ の合成の問題が出題されることがほとんどなので，

$\cos$ の合成が出題されたので戸惑った受験生が多かったのではないか

三角関数の合成は，加法定理の逆の計算である

ことを理解しておく必要がある

対策

(1) は三角関数の理解度をはかるにはちょうどよい問題

三角関数の合成から，最大値・最小値の問題は定番なので練習しておこう

　

(2) は三角関数の合成が加法定理の逆の計算であることを理解し

その手順で三角関数の合成ができるようになる必要がある

\begin{eqnarray} y &=& \sin\theta+\sqrt{3}\cos\theta \\\\ &=& 2\left(\sin\theta\cdot\frac{1}{2}+\cos\theta\cdot\frac{\sqrt{3}}{2}\right) \\\\ &=& 2\left(\sin\theta\cos\frac{\pi}{3}+\cos\theta\sin\frac{\pi}{3}\right) \\\\ &=& 2\sin \left(\theta+\frac{\pi}{3}\right) \\\\ \end{eqnarray}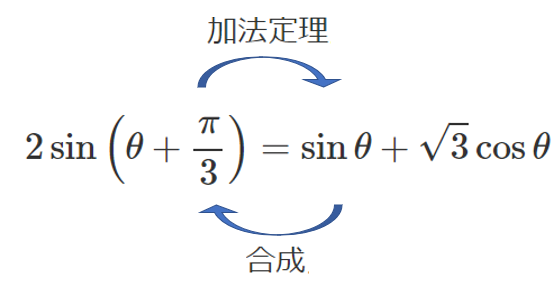

解答

(1)

　

　三角関数の値より，

$\displaystyle{\sin\frac{\pi}{\boxed{\mathbf{3}}}=\frac{\sqrt{3}}{2}}$，$\displaystyle{\cos\frac{\pi}{\boxed{\mathbf{3}}}=\frac{1}{2}}$

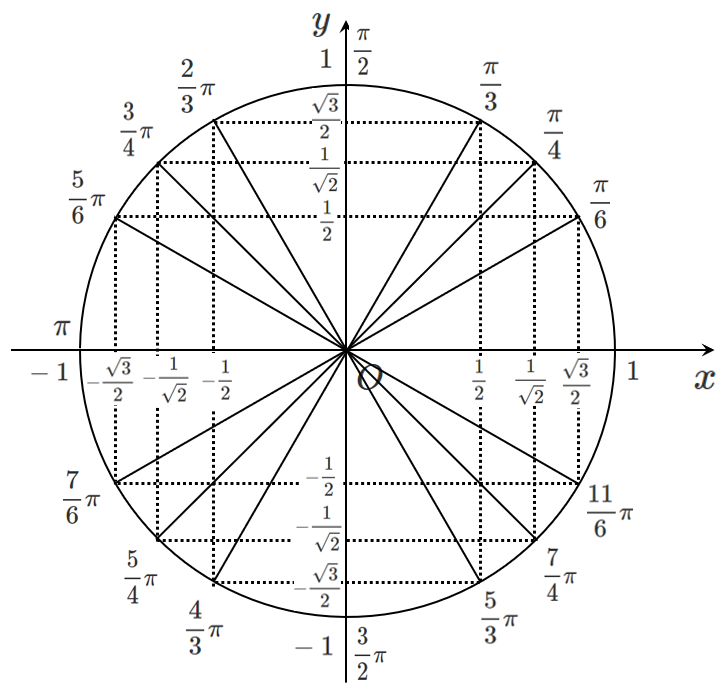
　単位円（半径が $1$ の円）における $\sin$ は $y$ 座標，$\cos$ は $x$ 座標

　

　三角関数の合成を計算で表すと

\begin{eqnarray} y &=& \sin\theta+\sqrt{3}\cos\theta　\cdots\cdots　(Ⅰ) \\\\ &=& 2\left(\sin\theta\cdot\frac{1}{2}+\cos\theta\cdot\frac{\sqrt{3}}{2}\right)　\cdots\cdots　(Ⅱ) \\\\ &=& 2\left(\sin\theta\cos\frac{\pi}{3}+\cos\theta\sin\frac{\pi}{3}\right)　\cdots\cdots　(Ⅲ) \\\\ &=& \boxed{\mathbf{2}}\sin \left(\theta+\frac{\pi}{\boxed{\mathbf{3}}}\right)　\cdots\cdots　(Ⅳ) \\\\ \end{eqnarray}

　(Ⅰ) から (Ⅱ) は，$\sin\theta$ の係数 $1$ と $\cos\theta$ の係数 $\sqrt{3}$ を用いて

$\sqrt{1^2+(\sqrt{3})^2}=2$

　$\sin\theta+\sqrt{3}\cos\theta$ を $2$ でくくると (Ⅱ) の式ができる

　

　(Ⅱ) から (Ⅲ) は， $\displaystyle{\sin\frac{\pi}{\boxed{\mathbf{3}}}=\frac{\sqrt{3}}{2}}$，$\displaystyle{\cos\frac{\pi}{\boxed{\mathbf{3}}}=\frac{1}{2}}$ を用いる

　

　(Ⅲ) から (Ⅳ) は，加法定理

$\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$

　を用いる

　

　

　

　三角関数の合成より，

\begin{eqnarray} y &=& \sin\theta+\sqrt{3}\cos\theta \\\\ &=& \boxed{\mathbf{2}}\sin \left(\theta+\frac{\pi}{\boxed{\mathbf{3}}}\right) \end{eqnarray}

　

　$\displaystyle{y=2\sin \left(\theta+\frac{\pi}{3}\right)}$ の最大値を求める

　$\displaystyle{\theta+\frac{\pi}{3}}$ の範囲は，$\displaystyle{0 ≦ \theta ≦\frac{\pi}{2}}$ より，

$\displaystyle{0 ≦ \theta ≦\frac{\pi}{2}}$

$\displaystyle{\frac{\pi}{3} ≦ \theta+\frac{\pi}{3} ≦\frac{\pi}{2}+\frac{\pi}{3}}$

$\displaystyle{\frac{\pi}{3} ≦ \theta+\frac{\pi}{3} ≦\frac{5}{6}\pi}$

　 $\displaystyle{\frac{\pi}{3} ≦ \theta+\frac{\pi}{3} ≦\frac{5}{6}\pi}$ において $\displaystyle{y=2\sin \left(\theta+\frac{\pi}{3}\right)}$ の最大値を求める

　

　

　

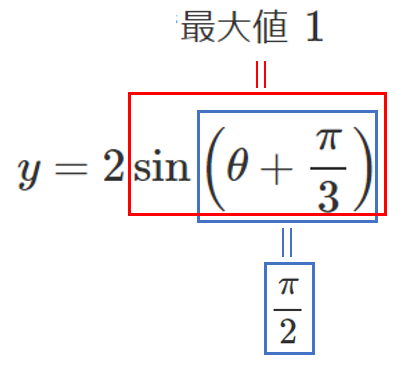
　 $\displaystyle{\sin \left(\theta+\frac{\pi}{3}\right)}$　は　$\displaystyle{\theta+\frac{\pi}{3}=\frac{\pi}{2}}$　で最大値 $1$ をとる

　すなわち

　 $\displaystyle{\sin \left(\theta+\frac{\pi}{3}\right)}$　は　$\displaystyle{\theta=\frac{\pi}{6}}$　で最大値 $1$ をとる

　したがって，

$\displaystyle{y=2\sin \left(\theta+\frac{\pi}{3}\right)}$　は　$\displaystyle{\theta=\frac{\pi}{ \boxed{\mathbf{6}} }}$　で最大値 $ \boxed{\mathbf{2}} $ をとる

(2)

　

　(i)　$p=0$ のとき，　$y=\sin\theta$

　　$\displaystyle{0 ≦ \theta ≦\frac{\pi}{2}}$ より，

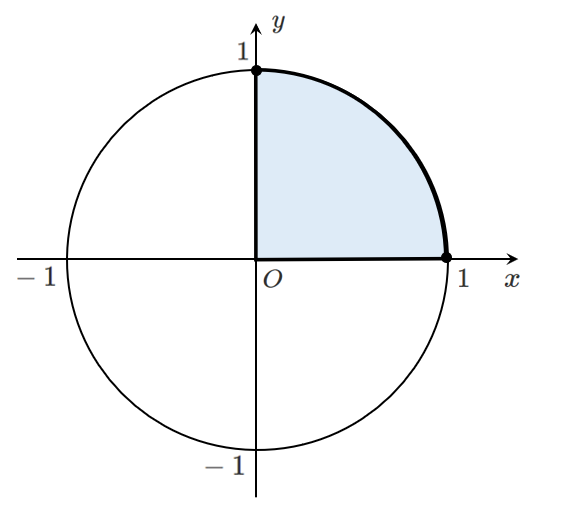
$y$ は $\displaystyle{\theta=\frac{\pi}{\boxed{\mathbf{2}}}}$ で最大値 $\boxed{\mathbf{1}}$ をとる

　

　

　(ii)　$p > 0$ のときは，

\begin{eqnarray} y &=& \sin\theta+p\cos\theta \\\\ &=& \sqrt{1^2+p^2}\left(\sin\theta\cdot\frac{1}{\sqrt{1^2+p^2}}+\cos\theta\cdot\frac{p}{\sqrt{1^2+p^2}}\right) \\\\ &=& \sqrt{1^2+p^2}\left(\sin\theta\cdot\frac{1}{\sqrt{1+p^2}}+\cos\theta\cdot\frac{p}{\sqrt{1+p^2}}\right) \end{eqnarray}

　　ここで，

$\displaystyle{\sin\alpha=\frac{1}{\sqrt{1+p^2}}}$，$\displaystyle{\cos\alpha=\frac{p}{\sqrt{1+p^2}}}$

　　となる角 $\alpha$ $\displaystyle{\left(0 < \theta < \frac{\pi}{2}\right)}$ を用いると

　

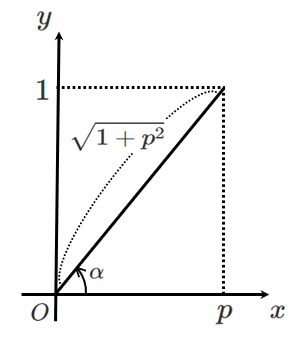
\begin{eqnarray} y &=& \sqrt{1^2+p^2}\left(\sin\theta\sin\alpha+\cos\theta\cos\alpha\right) \\\\ &=& \sqrt{1^2+p^2}\left(\cos\theta\cos\alpha+\sin\theta\sin\alpha\right) \end{eqnarray}

　

　　加法定理　$\cos(\theta-\alpha)=\cos\theta\cos\alpha+\sin\theta\sin\alpha$　より

$\displaystyle{y=\sqrt{\boxed{\mathbf{1+p^2}}}\cos(\theta-\alpha)}$

　　ただし，$\alpha$ は

　　　　　$\displaystyle{\sin\alpha=\frac{\boxed{\mathbf{1}}}{\sqrt{\boxed{\mathbf{1+p^2}}}}}$，$\displaystyle{\cos\alpha=\frac{\boxed{\mathbf{p}}}{\sqrt{\boxed{\mathbf{1+p^2}}}}}$

　　$\theta-\alpha$ の範囲は，$\displaystyle{0 ≦ \theta ≦\frac{\pi}{2}}$ より，

$\displaystyle{0 ≦ \theta ≦\frac{\pi}{2}}$

$ \displaystyle {-\alpha ≦ \theta-\alpha ≦ \frac{\pi}{2}-\alpha}$

　 $ \displaystyle {-\alpha ≦ \theta-\alpha ≦ \frac{\pi}{2}-\alpha}$ において $\displaystyle{y=\sqrt{1+p^2}\cos(\theta-\alpha)}$ の最大値を求める

　

　

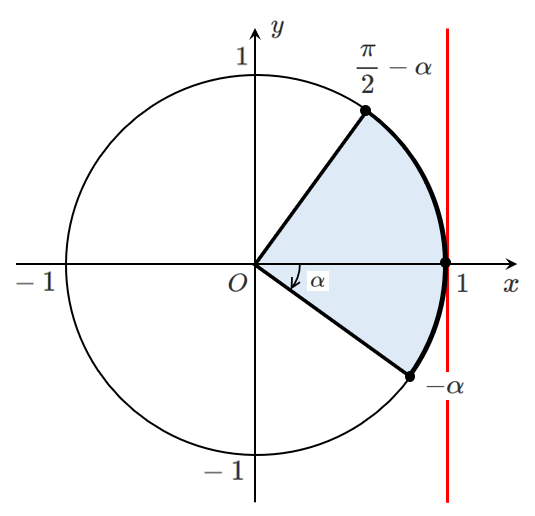
$\cos(\theta-\alpha)$ は　$\theta-\alpha=0$　で最大値 $1$ をとる

　　すなわち，

$\cos(\theta-\alpha)$ は　$\theta=-\alpha$　で最大値 $1$ をとる

　　したがって，

$\displaystyle{y=\sqrt{1+p^2}\cos(\theta-\alpha)}$ は　$\theta= \boxed{\mathbf{-\alpha}} $　で最大値 $ \boxed{\mathbf{\sart{1+p^2}}}$ をとる

　

　(iii)　$p < 0$ のとき，

　　$p=-q$ $(q>0)$ とすると

$\displaystyle{y=\sin\theta-q\cos\theta}$

　　$\displaystyle{0 ≦ \theta ≦ \frac{\pi}{2}}$ において $\theta$ が増えるにつれて，

$\sin\theta$ は増加，$\cos\theta$ は減少

　　するので，$y$ の値は増加する

　　よって，$y$ は　$\displaystyle{\theta=\frac{\pi}{2}}$　で最大値をとる

　　したがって，

$y$ は $\displaystyle{\theta=\boxed{\mathbf{\frac{\pi}{2}}}}$ で最大値 $\boxed{\mathbf{1}}$ をとる。

問われる力

• 三角関数の値
• 三角関数の合成
• 加法定理
• 三角関数の最大

2021年度共通テストの大問

2021年度共通テスト数学ⅠA

• 第１問【１】数と式
• 第１問【２】図形と計量
• 第２問【１】２次関数
• 第２問【２】データの分析
• 第３問　　　場合の数と確率
• 第４問　　　整数の性質
• 第５問　　　図形の性質

2021年度共通テスト数学ⅡB

• 第１問【１】三角関数
• 第１問【２】指数関数・対数関数
• 第２問　　　微分法・積分法
• 第３問　　　確率分布と統計的な推測
• 第４問　　　数列
• 第５問　　　ベクトル